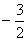题目内容
已知数列{an}是等差数列,{bn}是等比数列,其中a1=b1=1,a2≠b2,且b2为a1,a2的等差中项,a2为b2,b3的等差中项.
(1)求数列{an}与{bn}的通项公式;
(2)记cn=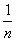 (a1+a2+…+an)(b1+b2+…+bn),求数列{cn}的前n项和Sn.
(a1+a2+…+an)(b1+b2+…+bn),求数列{cn}的前n项和Sn.
解:(1)设{an}的公差为d,{bn}的公比为q.
由2b2=a1+a2,2a2=b2+b3,
得q=1,d=0或q=2,d=2,
又a2≠b2,所以q=2,d=2,
所以an=2n-1,bn=2n-1.
(2)由(1),得
cn=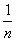 ·n2·(2n-1)=n·2n-n,
·n2·(2n-1)=n·2n-n,
所以Sn=(1×21+2×22+…+n×2n)-(1+2+…+n).
令Tn=1×21+2×22+…+n×2n,①
2Tn=1×22+2×23+…+n×2n+1,②
由②-①,得Tn=(n-1)·2n+1+2,
所以Sn=(n-1)·2n+1-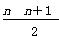 +2.
+2.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (
(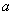 >0,
>0,  , 则
, 则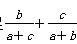 ≥1,则角A的范围是( )
≥1,则角A的范围是( )
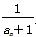 ,记Sn为数列{an}的前n项和,则S2 014=________.
,记Sn为数列{an}的前n项和,则S2 014=________.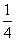 C.
C.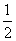 D.1
D.1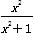 ,则f(1)+f(2)+…+f(2 013)+f(2 014)+
,则f(1)+f(2)+…+f(2 013)+f(2 014)+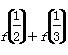 +…+
+…+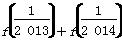 =( )
=( )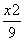 -
-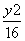 =1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )
=1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )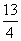 或
或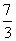 B.
B.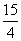 或
或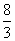 C.
C.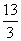 D.
D.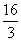
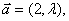 若
若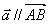 , 则实数
, 则实数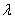 的值为( )
的值为( )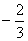 B.
B. 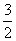 C.
C. 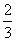 D.
D.