题目内容
8.直线过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点,斜率为2,若与双曲线的两个交点分别在左右两支上,则双曲线离心率e的取值范围是( )| A. | $e>\sqrt{2}$ | B. | $1<e<\sqrt{3}$ | C. | $e>\sqrt{5}$ | D. | $1<e<\sqrt{5}$ |
分析 根据已知直线的斜率,求出渐近线的斜率范围,推出a,b的关系,然后求出离心率的范围.
解答 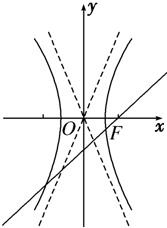 解:依题意,斜率为2的直线l过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$,
解:依题意,斜率为2的直线l过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$,
的右焦点且与双曲线的左右两支分别相交,
结合图形分析可知,双曲线的一条渐近线的斜率$\frac{b}{a}$必大于2,
即$\frac{b}{a}$>2,
因此该双曲线的离心率e=$\frac{c}{a}$═$\sqrt{1+(\frac{b}{a})^{2}}$>$\sqrt{1+4}$=$\sqrt{5}$.
故选:C.
点评 本题考查双曲线的方程和性质,主要是离心率的求法,注意运用直线的斜率,考查转化思想,是中档题.

练习册系列答案
相关题目
11.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接收雨水.如果某个天池盆的盆口直径为盆底直径的两倍,盆深为h(单位:寸),则该天池盆可测量出平面降雨量的最大值为(单位:寸)
提示:上、下底面圆的半径分别为R、r,高为h的圆台的体积的计算公式为V=$\frac{1}{3}$πh(R2+r2+Rr)( )
提示:上、下底面圆的半径分别为R、r,高为h的圆台的体积的计算公式为V=$\frac{1}{3}$πh(R2+r2+Rr)( )
| A. | $\frac{7}{12}$h | B. | $\frac{3}{4}$h | C. | $\frac{1}{2}$h | D. | h |
13.tan1020°=( )
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
20.已知cosα=$\frac{1}{3}$,α∈(0,π),则cos($\frac{3}{2}$π+2α)等于( )
| A. | $-\frac{{4\sqrt{2}}}{9}$ | B. | $-\frac{7}{9}$ | C. | $\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |