题目内容
已知椭圆的准线平行于x轴，长轴长是短轴长的3倍，且过点（2，3）．（Ⅰ）求椭圆的离心率；
（Ⅱ）求椭圆的标准方程，并写出准线方程．
【答案】分析：（I）设椭圆的方程是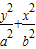 
=1，根据长轴长是短轴长的3倍，求出a与b，c与b的关系，求出椭圆的离心率；
（II）设椭圆的方程是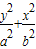
=1，由题设，中心在坐标原点的椭圆过点（2，3），且它的长轴长是短轴长的3倍，故可以得两个关于a，b，c的方程，解出参数就可得到椭圆的方程及准线方程．
解答：解：（Ⅰ）设椭圆的方程是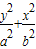
=1，
∵长轴长是短轴长的3倍，
∴a=3b，
∴c=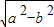
=2
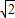b，
∴椭圆的离心率为：
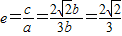（4分）
（Ⅱ）由题设，中心在坐标原点的椭圆过点（2，3），且a=3b，
∴
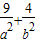=1，又a2=c2+b2
三式联立可以解得a=3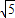
，b=
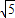，c=2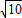
，
故该椭圆的方程为：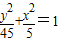
（6分），
准线：
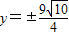（2分）
点评：本题考查椭圆的几何特征，利用几何特征建立三个参数a，b，c的方程，求出参数，进而求出椭圆的方程．
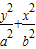=1，根据长轴长是短轴长的3倍，求出a与b，c与b的关系，求出椭圆的离心率； （II）设椭圆的方程是
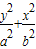=1，由题设，中心在坐标原点的椭圆过点（2，3），且它的长轴长是短轴长的3倍，故可以得两个关于a，b，c的方程，解出参数就可得到椭圆的方程及准线方程．解答：解：（Ⅰ）设椭圆的方程是
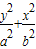=1，∵长轴长是短轴长的3倍，
∴a=3b，
∴c=
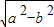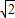=2b，∴椭圆的离心率为：
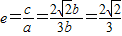（4分）（Ⅱ）由题设，中心在坐标原点的椭圆过点（2，3），且a=3b，
∴
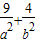=1，又a2=c2+b2三式联立可以解得a=3
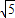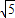，b=，c=2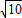，故该椭圆的方程为：
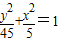（6分），准线：
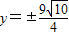（2分）点评：本题考查椭圆的几何特征，利用几何特征建立三个参数a，b，c的方程，求出参数，进而求出椭圆的方程．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
，其焦点F（c，0）（c＞0）对应的准线l与x轴交于A点，|OF|=2|FA|，过A的直线与椭圆交于P、Q两点.
，求直线PQ的方程； （3）设
，过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.