题目内容
如图,四边形ABCD与四边形 都为正方形,
都为正方形, ,F
,F
为线段 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.
(1)当E为线段BC中点时,求证: 平面AEF;
平面AEF;
(2)求证:平面AEF
 平面;
平面;
(3)设 ,写出
,写出 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明).
(1)证明过程详见解析;(2)证明过程详见解析;(3) .
.
解析试题分析:本题主要考查线面平行、线面垂直、面面垂直等基础知识,考查学生的空间想象能力、逻辑推理能力.第一问,在三角形BCN中,利用EF为中位线,得到 ,再利用线面平行的判定得
,再利用线面平行的判定得 平面AEF;第二问,利用2个正方形ABCD和ADMN,得
平面AEF;第二问,利用2个正方形ABCD和ADMN,得

 ,
,

 ,利用线面垂直的判定得
,利用线面垂直的判定得
 平面
平面 ,利用线面垂直的性质得
,利用线面垂直的性质得

 ,在三角形ABN中,
,在三角形ABN中, ,利用线面垂直的判定,得
,利用线面垂直的判定,得
 平面
平面 ,利用面面垂直的判定得平面AEF
,利用面面垂直的判定得平面AEF 平面BCMN;第三问,根据图形写出结论.
平面BCMN;第三问,根据图形写出结论.
试题解析:(1)证明:F为线段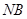 的中点,E为线段BC中点,所以
的中点,E为线段BC中点,所以 ,
,
又 平面AEF,
平面AEF, 平面AEF
平面AEF
所以 平面AEF 4分
平面AEF 4分
(2)证明:四边形 与四边形
与四边形 都为正方形
都为正方形
所以

 ,
,



 ,所以
,所以
 平面
平面
 平面
平面 ,故
,故


 ,所以
,所以
由题意 =
= ,F为线段
,F为线段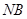 的中点
的中点
所以
 ,所以
,所以
 平面
平面
 平面AEF
平面AEF
所以平面AEF 平面
平面 . -11分
. -11分
(3) 14分
14分
考点:线面平行、线面垂直、面面垂直.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目

 中,
中, ,
, ,且
,且 .
. 为一边向梯形外作正方形
为一边向梯形外作正方形 ,然后沿边
,然后沿边 为
为 的中点,如图2.
的中点,如图2.

 ∥平面
∥平面 ;
; ;
; 到平面
到平面 中,
中, ,
, .若
.若 为
为 的中点,求直线
的中点,求直线 与平面
与平面 所成的角.
所成的角.

 中,
中, ,
, ,
, ,点
,点 为
为 中点.将
中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面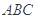 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
 上找一点
上找一点 ,使
,使 平面
平面 ;
; 到平面
到平面 的距离.
的距离.
 中,
中, ,斜边
,斜边 .
. 可以通过
可以通过 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角.动点
是直二面角.动点 在斜边
在斜边 上.
上.
 平面
平面 ;
; 与平面
与平面
 的值..
的值..