题目内容
如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证:
(1)EF//平面MNCB;
(2)平面MAC 平面BND.
平面BND.
(1) (2)见解析
解析试题分析:(1)取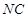 的中点
的中点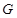 ,连接
,连接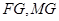 ,欲证
,欲证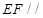 平面
平面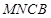 ,只要证
,只要证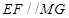
只要证四边形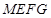 是平行四边形即可,事实上,由于
是平行四边形即可,事实上,由于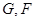 分别是
分别是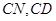 的中点,易知
的中点,易知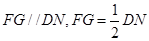 另一方面又有
另一方面又有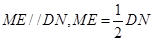 ,所以FG与ME平行且相等,四边形
,所以FG与ME平行且相等,四边形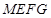 是平行四边形,问题得证.
是平行四边形,问题得证.
(2) 连接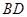 、
、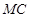 ,欲证
,欲证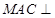 平面
平面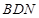 ,只要证
,只要证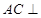 平面
平面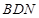 ,即证
,即证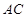 与平面
与平面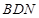 内的两条相交直线
内的两条相交直线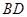 、
、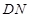 都垂直;由菱形
都垂直;由菱形 易知
易知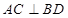 ;另外,由平面
;另外,由平面 平面
平面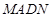
及矩形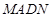 易证
易证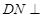 平面
平面 ,进而有
,进而有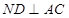 ,所以问题得证.
,所以问题得证.
试题解析:
证明:(1)取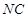 的中点
的中点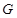 ,连接
,连接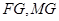 ,
,
因为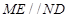 且
且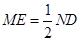 ,
,
又因为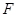 、
、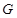 分别为
分别为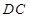 、
、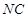 的中点,
的中点,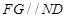 且
且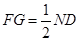 , 2分
, 2分
所以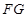 与
与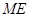 平行且相等,所以四边形
平行且相等,所以四边形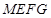 是平行四边形,
是平行四边形,
所以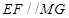 , 4分
, 4分
又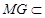 平面
平面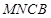 ,
,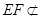 平面
平面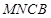 ,
,
所以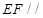 平面
平面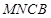 6分
6分
(2)连接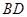 、
、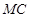 ,因为四边形
,因为四边形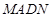 是矩形,
是矩形,
所以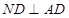 ,又因为平面
,又因为平面 平面
平面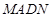
所以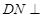 平面
平面 8分
8分
所以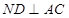
因为四边形 是菱形,所以
是菱形,所以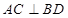
因为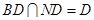 ,所以
,所以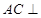

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 .
.
 所成的角的大小.
所成的角的大小.
 ,求线段AM的长.
,求线段AM的长.
 的值;
的值;
 中,
中, ,
, ,且
,且 .
. 为一边向梯形外作正方形
为一边向梯形外作正方形 ,然后沿边
,然后沿边 为
为 的中点,如图2.
的中点,如图2.

 ∥平面
∥平面 ;
; ;
; 到平面
到平面 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,
, ,
, .
.
 平面
平面 ;
; 平面
平面 .
. 中,
中, ,
, .若
.若 为
为 的中点,求直线
的中点,求直线 与平面
与平面 所成的角.
所成的角.
 中,
中, ,
, ,
, ,点
,点 为
为 中点.将
中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面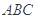 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
 上找一点
上找一点 ,使
,使 平面
平面 ;
; 到平面
到平面 的距离.
的距离. ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
 ;若不存在,说明理由.
;若不存在,说明理由.