题目内容
(本小题满分10分)选修4-5:不等式选讲
设关于 的不等式
的不等式 .
.
(I) 当 ,解上述不等式。
,解上述不等式。
(II)若上述关于 的不等式有解,求实数
的不等式有解,求实数 的取值范围。
的取值范围。
设关于
 的不等式
的不等式 .
.(I) 当
 ,解上述不等式。
,解上述不等式。(II)若上述关于
 的不等式有解,求实数
的不等式有解,求实数 的取值范围。
的取值范围。(I)  ;(II)
;(II) 。
。
 ;(II)
;(II) 。
。试题分析:(I) 当
 ,上述不等式为
,上述不等式为 ,等价于
,等价于①
 或 ②
或 ②
由得①
 ,由得②
,由得② ;所以不等式解集为
;所以不等式解集为 。 …………5分
。 …………5分(II)解法一:
当x≥1时,不等式化为
 ,即x≤
,即x≤ .
. 这时不等式有解当且仅当1≤
 ,即a≥1.
,即a≥1. 当x<1时,不等式化为
 ,即1≤a,这时不等式有解当且仅当a≥1.
,即1≤a,这时不等式有解当且仅当a≥1. 综上所述,关于x的不等式
 ≤a有解,
≤a有解,则实数a的取值范围是
 . ………10分
. ………10分解法二:不等式
 等价于
等价于
设
 ,则
,则
易知
 的最小值为1。
的最小值为1。关于
 的不等式
的不等式 有解,即
有解,即 ≤a有解,所以a≥1。 ……10分
≤a有解,所以a≥1。 ……10分点评:解含绝对值不等式的主要方法:一是利用绝对值不等式的几何意义来求解,体现了数形结合的思想;二是利用“零点分段法”进行分段讨论,去掉绝对值符号,从而求解,体现了分类讨论的思想。三是通过构造函数,利用函数的图像来求解,体现了函数与方程的思想。

练习册系列答案
相关题目
 ,则
,则 的大小关系为
的大小关系为



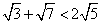
 的解集为
的解集为 .
. ,试比较
,试比较  与
与  的大小.
的大小.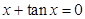 的正根从小到大地依次排列为
的正根从小到大地依次排列为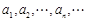 ,
,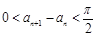 ; ②
; ②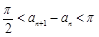 ;
;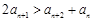 ; ④
; ④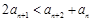 ;
; ,
,
 的前提下,求a的一个值,是它成为
的前提下,求a的一个值,是它成为 的一个充分但不必要条件。
的一个充分但不必要条件。 ,则“
,则“ ”是“
”是“ ”的 条件.
”的 条件.  ,且
,且 <0,a="f" (
<0,a="f" ( ),b="f" (
),b="f" ( ),c="f" (
),c="f" ( ),则a,b,c的大小关系为
),则a,b,c的大小关系为 ,
, ,则下列不等式中恒成立的是( )
,则下列不等式中恒成立的是( )


