题目内容
某校为了解高二学生 、
、 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试 、
、 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2 2列联表:
2列联表:
|
|
|
|
合计 |
|
|
40 |
20 |
60 |
|
|
20 |
30 |
50 |
|
合计 |
60 |
50 |
110 |
(1)据此表格资料,你认为有多大把握认为“ 学科合格”与“
学科合格”与“ 学科合格”有关;
学科合格”有关;
(2)从“ 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“ 学科合格”的人数为
学科合格”的人数为 ,求
,求 的数学期望.
的数学期望.
附公式与表:

|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
【答案】
(1)有99%把握认为“ 学科合格”与“
学科合格”与“ 学科合格”有关
学科合格”有关
(2)
|
|
|
1 |
2 |
|
|
|
|
|

【解析】
试题分析:解:(1) 3分
3分
故认为有99%把握认为“ 学科合格”与“
学科合格”与“ 学科合格”有关 5分
学科合格”有关 5分
(2) 服从超几何分布,
服从超几何分布, 7分
7分



随机变量 的分布列为:
的分布列为:
|
|
|
1 |
2 |
|
|
|
|
|

答:随机变量 的数学期望是
的数学期望是 12分
12分
考点:分布列和独立性检验
点评:主要是考查了分布列的性质以及运用独立性检验的公式判定变量的相关性,属于基础题。

练习册系列答案
相关题目
某校为了解高二学生A,B两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试A,B两个学科的合格人数与不合格人数,得到以下2X2列联表:
(1)据此表格资料,你认为有多大把握认为“A学科合格”与“B学科合格”有关;
(2)从“A学科合格”的学生中任意抽取2人,记被抽取的2名学生中“B学科合格”的人数为X,求X的数学期望.
附公式与表:K2=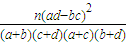
| A学科合格人数 | A学科不合格人数 | 合计 | |
| B学科合格人数 | 40 | 20 | 60 |
| B学科不合格人数 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
(2)从“A学科合格”的学生中任意抽取2人,记被抽取的2名学生中“B学科合格”的人数为X,求X的数学期望.
附公式与表:K2=
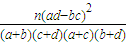
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
某校为了解高二学生A,B两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试A,B两个学科的合格人数与不合格人数,得到以下2X2列联表:
(1)据此表格资料,你认为有多大把握认为“A学科合格”与“B学科合格”有关;
(2)从“A学科合格”的学生中任意抽取2人,记被抽取的2名学生中“B学科合格”的人数为X,求X的数学期望.
附公式与表:K2=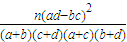
| A学科合格人数 | A学科不合格人数 | 合计 | |
| B学科合格人数 | 40 | 20 | 60 |
| B学科不合格人数 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
(2)从“A学科合格”的学生中任意抽取2人,记被抽取的2名学生中“B学科合格”的人数为X,求X的数学期望.
附公式与表:K2=
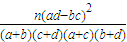
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |






