题目内容
某校为了解高二学生A,B两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试A,B两个学科的合格人数与不合格人数,得到以下2X2列联表:| A学科合格人数 | A学科不合格人数 | 合计 | |
| B学科合格人数 | 40 | 20 | 60 |
| B学科不合格人数 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
(2)从“A学科合格”的学生中任意抽取2人,记被抽取的2名学生中“B学科合格”的人数为X,求X的数学期望.
附公式与表:K2=
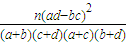
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【答案】分析:(1)利用公式先计算出K2,即可得出答案;
(2)由题意可知:X可以取0,1,2.因为A学科合格的人数为60,从中任选2人可有 种方法,其中X=0表示所抽取的2人A学科合格而B学科不合格,故有
种方法,其中X=0表示所抽取的2人A学科合格而B学科不合格,故有 种选法;X=1表示所抽取的2人A学科合格而B学科有1人合格1人不合格,故有
种选法;X=1表示所抽取的2人A学科合格而B学科有1人合格1人不合格,故有 种选法;X=2表示所抽取的2人A学科合格而B学科也合格,故有
种选法;X=2表示所抽取的2人A学科合格而B学科也合格,故有 种选法.再利用古典概型的概率计算公式即可得出.进而得到分布列和数学期望.
种选法.再利用古典概型的概率计算公式即可得出.进而得到分布列和数学期望.
解答:解:(1)K2= ≈7.822>6.635
≈7.822>6.635
所以,有90%的把握认为“A学科合格”与“B学科合格”有关.
(2)由题意可知:X可以取0,1,2,
P(X=0)= =
= ,P(X=1)=
,P(X=1)= =
= ,P(X=2)=
,P(X=2)= =
=
∴EX= +2×
+2× =
= .
.
点评:熟练掌握古典概型的概率计算公式、随机变量的分布列和数学期望、独立性检验的方法是解题的关键.
(2)由题意可知:X可以取0,1,2.因为A学科合格的人数为60,从中任选2人可有
 种方法,其中X=0表示所抽取的2人A学科合格而B学科不合格,故有
种方法,其中X=0表示所抽取的2人A学科合格而B学科不合格,故有 种选法;X=1表示所抽取的2人A学科合格而B学科有1人合格1人不合格,故有
种选法;X=1表示所抽取的2人A学科合格而B学科有1人合格1人不合格,故有 种选法;X=2表示所抽取的2人A学科合格而B学科也合格,故有
种选法;X=2表示所抽取的2人A学科合格而B学科也合格,故有 种选法.再利用古典概型的概率计算公式即可得出.进而得到分布列和数学期望.
种选法.再利用古典概型的概率计算公式即可得出.进而得到分布列和数学期望.解答:解:(1)K2=
 ≈7.822>6.635
≈7.822>6.635所以,有90%的把握认为“A学科合格”与“B学科合格”有关.
(2)由题意可知:X可以取0,1,2,
P(X=0)=
 =
= ,P(X=1)=
,P(X=1)= =
= ,P(X=2)=
,P(X=2)= =
=
∴EX=
 +2×
+2× =
= .
.点评:熟练掌握古典概型的概率计算公式、随机变量的分布列和数学期望、独立性检验的方法是解题的关键.

练习册系列答案
相关题目
为了了解某校1503名高二学生的学业负担情况,从中抽取一个容量为50的样本,现在用系统抽样的方法,需要从总体中剔除3个个体,在整个抽样过程中,每个个体被剔除的可能性和每个个体被抽取的可能性分别是( )
某校为了解高二学生A,B两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试A,B两个学科的合格人数与不合格人数,得到以下2X2列联表:
(1)据此表格资料,你认为有多大把握认为“A学科合格”与“B学科合格”有关;
(2)从“A学科合格”的学生中任意抽取2人,记被抽取的2名学生中“B学科合格”的人数为X,求X的数学期望.
附公式与表:K2=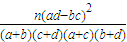
| A学科合格人数 | A学科不合格人数 | 合计 | |
| B学科合格人数 | 40 | 20 | 60 |
| B学科不合格人数 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
(2)从“A学科合格”的学生中任意抽取2人,记被抽取的2名学生中“B学科合格”的人数为X,求X的数学期望.
附公式与表:K2=
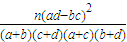
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |