题目内容
在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,向量
的对边,向量 ,
, ,且
,且 //
// .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当 时,
时, 的最大值为
的最大值为 ;当
;当 时,
时, 的最小值为
的最小值为 .
.
解析试题分析:(Ⅰ)求角 的大小,由已知
的大小,由已知 //
// ,根据共线向量的充要条件可知,
,根据共线向量的充要条件可知, ,这样得到的关系式即含有边,又含有角,需要进行边角互化,由于求B角的值,故利用正弦定理把边化成角,得
,这样得到的关系式即含有边,又含有角,需要进行边角互化,由于求B角的值,故利用正弦定理把边化成角,得 ,通过三角恒等变化,从而求出
,通过三角恒等变化,从而求出 ;(Ⅱ)求
;(Ⅱ)求 在区间
在区间 上的最大值和最小值,首先对
上的最大值和最小值,首先对 进行恒等变化,把它化为一个角的一个三角函数,由它的最小正周期为
进行恒等变化,把它化为一个角的一个三角函数,由它的最小正周期为 ,来确定
,来确定 的值
的值 ,得
,得 的解析式,从而求出最大值和最小值.
的解析式,从而求出最大值和最小值.
试题解析:(Ⅰ)由 //
// ,得
,得
 , 1分
, 1分
由正弦定理,得 3分
3分 6分
6分
(Ⅱ)由题知, , 8分
, 8分
由已知得 ,
, ,
, 9分
9分
当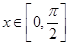 时,
时, 10分
10分
所以,当 时,
时, 的最大值为
的最大值为 ;当
;当 时,
时, 的最小值为
的最小值为 . 12分
. 12分
考点:解三角形,三角恒等变化,三角函数最值.

练习册系列答案
相关题目
 中,角
中,角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,已知
,已知 ,
, .
. ,求
,求 ,求
,求

 ;
;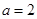 ,求
,求 面积S的最大值.
面积S的最大值. 的顶点
的顶点 ,顶点
,顶点 在直线
在直线 上;
上; 求点
求点 ,且
,且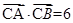 ,求角
,求角 分别是
分别是 的三个内角
的三个内角 的对边,
的对边, .
. 的大小;
的大小; 的值域.
的值域. 中,满足
中,满足 的夹角为
的夹角为 ,
, 是
是 的中点,
的中点,  ,求向量
,求向量 的夹角的余弦值;.
的夹角的余弦值;. ,点
,点 在边
在边 上且
上且 ,如果
,如果 ,求
,求 的值。
的值。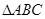 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足
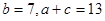 ,求
,求 的取值范围.
的取值范围. 中,
中, 分别为角
分别为角 所对的边,且
所对的边,且 ,
, ,
, ,求角
,求角 的正弦值.
的正弦值.