题目内容
证明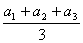 ,其中a1,a2,a3∈R.
,其中a1,a2,a3∈R.
证明:由柯西不等式得(a1+a2+a3)2=(a1·1+a2·1+a3·1)2≤(a12+a22+a32)·(12+12+12)=(a12+a22+a32)·3,
∴![]() ≤a12+a22+a32,
≤a12+a22+a32,
故![]() ≤
≤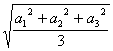 .
.

练习册系列答案
相关题目
题目内容
证明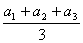 ,其中a1,a2,a3∈R.
,其中a1,a2,a3∈R.
证明:由柯西不等式得(a1+a2+a3)2=(a1·1+a2·1+a3·1)2≤(a12+a22+a32)·(12+12+12)=(a12+a22+a32)·3,
∴![]() ≤a12+a22+a32,
≤a12+a22+a32,
故![]() ≤
≤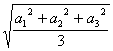 .
.
