题目内容
已知点B1(1,y1),B2(2,y2),…,Bn(n,yn),…(n∈N*)顺次为直线y=
+
上的点,点A1(x1,0),A2(x2,0),…An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.
(Ⅰ)证明:数列{yn}是等差数列;
(Ⅱ)求证:对任意的n∈N*,xn+2-xn是常数,并求数列{xn}的通项公式;
(Ⅲ)在上述等腰三角形AnBnAn+1中是否存在直角三角形,若存在,求出此时a的值;若不存在,请说明理由.
| x |
| 4 |
| 1 |
| 12 |
(Ⅰ)证明:数列{yn}是等差数列;
(Ⅱ)求证:对任意的n∈N*,xn+2-xn是常数,并求数列{xn}的通项公式;
(Ⅲ)在上述等腰三角形AnBnAn+1中是否存在直角三角形,若存在,求出此时a的值;若不存在,请说明理由.
分析:(Ⅰ)把Bn坐标代入直线方程可得yn=
+
,由等差数列定义可证;
(Ⅱ)由题意可得
=n,即xn+xn+1=2n,(n∈N*)①,又有xn+2+xn+1=2(n+1)②,②-①得xn+2-xn=2,则奇数项、偶数项均构成等差数列,分别求出即可;
(Ⅲ)当n为奇数、当n为偶数时可分别求得|AnAn+1|,作x轴垂线,垂足为Cn,要使等腰三角形AnBnAn+1为直角三角形,必须且只需|AnAn+1|=2|BnCn|,分n为奇数、偶数两种情况可求得a值;
| n |
| 4 |
| 1 |
| 12 |
(Ⅱ)由题意可得
| xn+xn+1 |
| 2 |
(Ⅲ)当n为奇数、当n为偶数时可分别求得|AnAn+1|,作x轴垂线,垂足为Cn,要使等腰三角形AnBnAn+1为直角三角形,必须且只需|AnAn+1|=2|BnCn|,分n为奇数、偶数两种情况可求得a值;
解答:解:(Ⅰ)依题意有yn=
+
,于是yn+1-yn=
.
所以数列{yn}是等差数列.
(Ⅱ)由An、Bn、An+1构成以Bn为顶点的等腰三角形,得
=n,即xn+xn+1=2n,(n∈N*)①,
所以又有xn+2+xn+1=2(n+1).②
由②-①得xn+2-xn=2,
可知x1,x3,x5,…;x2,x4,x6,…都是等差数列.
那么得x2k-1=x1+2(k-1)=2k+a-2,x2k=x2+2(k-1)=2-a+2(k-1)=2k-a.(k∈N*)
故xn=
;
(Ⅲ)当n为奇数时,An(n+a-1,0),An+1(n+1-a,0),所以|AnAn+1|=2(1-a);
当n为偶数时,An(n-a,0),An+1(n+a,0),所以|AnAn+1|=2a;
作x轴垂线,垂足为Cn,则|BnCn|=
+
,
要使等腰三角形AnBnAn+1为直角三角形,必须且只需|AnAn+1|=2|BnCn|.
当n为奇数时,有2(1-a)=2(
+
),即12a=11-3n.①
当n=1时,a=
;当n=3时,a=
;当n≥5,①式无解.
当n为偶数时,有12a=3n+1,同理可求得a=
.
综上所述,上述等腰三角形AnBnAn+1中存在直角三角形,此时a的值为
或
或
.
| n |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
所以数列{yn}是等差数列.
(Ⅱ)由An、Bn、An+1构成以Bn为顶点的等腰三角形,得
| xn+xn+1 |
| 2 |
所以又有xn+2+xn+1=2(n+1).②
由②-①得xn+2-xn=2,
可知x1,x3,x5,…;x2,x4,x6,…都是等差数列.
那么得x2k-1=x1+2(k-1)=2k+a-2,x2k=x2+2(k-1)=2-a+2(k-1)=2k-a.(k∈N*)
故xn=
|
(Ⅲ)当n为奇数时,An(n+a-1,0),An+1(n+1-a,0),所以|AnAn+1|=2(1-a);
当n为偶数时,An(n-a,0),An+1(n+a,0),所以|AnAn+1|=2a;
作x轴垂线,垂足为Cn,则|BnCn|=
| n |
| 4 |
| 1 |
| 12 |
要使等腰三角形AnBnAn+1为直角三角形,必须且只需|AnAn+1|=2|BnCn|.
当n为奇数时,有2(1-a)=2(
| n |
| 4 |
| 1 |
| 12 |
当n=1时,a=
| 2 |
| 3 |
| 1 |
| 6 |
当n为偶数时,有12a=3n+1,同理可求得a=
| 7 |
| 12 |
综上所述,上述等腰三角形AnBnAn+1中存在直角三角形,此时a的值为
| 2 |
| 3 |
| 1 |
| 6 |
| 7 |
| 12 |
点评:本题考查等差数列与函数的综合,考查学生分析问题解决问题的能力,考查分类讨论思想,知识点较多,能力要求较高.

练习册系列答案
相关题目
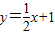 上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn,
上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn, 前n项和为Tn,判断Tn与
前n项和为Tn,判断Tn与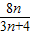 (n∈N*)的大小,并证明你的结论.
(n∈N*)的大小,并证明你的结论.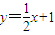 上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn,
上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn, 前n项和为Tn,判断Tn与
前n项和为Tn,判断Tn与 (n∈N*)的大小,并证明你的结论.
(n∈N*)的大小,并证明你的结论.