题目内容
【题目】如图，A1 ， A2为椭圆 
=1的长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1 ， A2的三点，直线QA1 ， QA2 ， OS，OT围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ） 
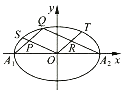
A.5
B.3+ 
C.9
D.14
【答案】D
【解析】解：设Q（x0 ， y0），则 
=1，∴ 
= 
．设直线OS，OT的方程分别为：y=k1x，y=k2x，
则 
=k1 ， 
=k2 ．
∵ = 
= 
=﹣ 
．
∴k1k2=﹣ ．
联立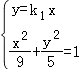 
，解得 
= 
， 
= 
．
同理可得： 
= 
， 
= 
．
∴|OS|2+|OT|2= + + + = + + +
= 
+ 
= 
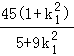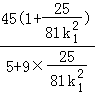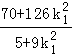=14．
故选：D．
设Q（x0 ， y0），则 =1，可得： =﹣ 
．设直线OS，OT的方程分别为：y=k1x，y=k2x，则 =k1 ， =k2 ． 可得k1k2 ． 直线方程与椭圆方程分别联立可得 ， ； ， ．即可得出：|OS|2+|OT|2 ．
练习册系列答案
相关题目
