题目内容
.已知向量a=(2cos x,1),b=(cos x, sin 2x),函数f(x)=a·b.
sin 2x),函数f(x)=a·b.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[ ,
, ]时,若f(x)=
]时,若f(x)= ,求f(x-
,求f(x- )的值.
)的值.
解:(1)f(x)=2cos2x+ sin 2x=2sin(2x+
sin 2x=2sin(2x+ )+1,
)+1,
∴T=π.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,得kπ-
,得kπ- ≤x≤kπ+
≤x≤kπ+ (k∈Z),则f(x)的单调递增区间为[kπ-
(k∈Z),则f(x)的单调递增区间为[kπ- ,kπ+
,kπ+ ](k∈Z).
](k∈Z).
(2)f(x)=2sin(2x+ )+1=
)+1= ,则sin(2x+
,则sin(2x+ )=
)= .
.
由 ≤x≤
≤x≤ ,得
,得 ≤2x+
≤2x+ ≤
≤ ,
,
所以cos(2x+ )=-
)=- =-
=- ,
,
f(x- )=2sin(2x+
)=2sin(2x+ -
- )+1
)+1
=2sin(2x+ )cos
)cos  -2cos(2x+
-2cos(2x+ )sin
)sin  +1
+1
=2× ×
× -2×(-
-2×(- )×
)× +1
+1
= .
.

练习册系列答案
相关题目
 )+2a+b,当x∈[0,
)+2a+b,当x∈[0, ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1.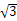 sin ωx+cos ωx+c(ω>0,x∈R,c是实数常数)的图象上的一个最高点是(
sin ωx+cos ωx+c(ω>0,x∈R,c是实数常数)的图象上的一个最高点是( ,1),与该最高点最近的一个最低点是(
,1),与该最高点最近的一个最低点是(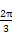 ,-3),
,-3),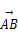 ·
·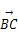 =-
=- ac,角A的取值范围是区间M,当x∈M时,试求函数f(x)的取值范围.
ac,角A的取值范围是区间M,当x∈M时,试求函数f(x)的取值范围. ,cos(α-β)=
,cos(α-β)= ,则c等于( )
,则c等于( ) (C)3 (D)
(C)3 (D)
 ,
, ,
, ,
, 满足等式
满足等式 ,
, .若
.若 ,则实数
,则实数  _______.
_______.