题目内容
9.己知tanα=-$\frac{1}{3}$,求下列各式的值:(1)$\frac{3sinα+2cosα}{6sinα-5cosα}$;
(2)$\frac{si{n}^{2}α-2co{s}^{2}α}{6sinαcosα+co{s}^{2}α}$;
(3)sin2α-2cos2α
分析 (1)分子分母同时除以cosα,由此能求出结果.
(2)分子分母同时除以cos2α,由此能求出结果.
(3)sin2α-2cos2α等价转化为$\frac{si{n}^{2}α-2co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$后,分子分母同时除以cos2α,由此能求出结果.
解答 解:(1)∵tanα=-$\frac{1}{3}$,
∴$\frac{3sinα+2cosα}{6sinα-5cosα}$=$\frac{3tanα+2}{6tanα-5}$=$\frac{-1+2}{-2-5}$=-$\frac{1}{7}$.
(2)$\frac{si{n}^{2}α-2co{s}^{2}α}{6sinαcosα+co{s}^{2}α}$=$\frac{ta{n}^{2}α-2}{6tanα+1}$=$\frac{\frac{1}{9}-2}{-2+1}$=$\frac{17}{9}$.
(3)sin2α-2cos2α=$\frac{si{n}^{2}α-2co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α-2}{ta{n}^{2}α+1}$=$\frac{\frac{1}{9}-2}{\frac{1}{9}+1}$=-$\frac{17}{10}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意同角三角函数关系式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.要得到函数y=sin(-$\frac{1}{2}$x)的图象,只需将函数y=sin(-$\frac{1}{2}$x+$\frac{π}{6}$)的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
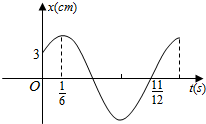 如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求:
如图,单摆从某点开始来回摆动,离开平衡位置的距离s(cm)和时间t(s)的函数关系是s=Asin(ωt+φ),0<φ<$\frac{π}{2}$,根据图象,求: