题目内容
3.甲乙二人玩猜字游戏,先由甲在心中想好一个数字,记作a,然后再由乙猜甲刚才所想到的数字,并把乙猜到的数字记为b,二人约定:a、b∈{1,2,3,4},且当|a-b|≤1时乙为胜方,否则甲为胜方.则甲取胜的概率是$\frac{3}{8}$.分析 本题是一个等可能事件的概率,试验发生包含的事件是两个人分别从4个数字中各选一个数字,共有4×4种结果,满足条件的事件是|a-b|≤1,可以列举出所有的满足条件的事件,根据概型概率公式得到结果.
解答 解:甲猜一数字有4种选择,乙任猜一数字也有4种选择,共有不同的配对方法4×4=16种,
其中,甲猜1或4时,乙猜3、4或1、2时甲胜,甲猜2或3时,乙猜4或1甲胜,
故甲取胜的方法数是2×2+2×1=6种,
即取胜的概率是$\frac{6}{16}=\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 本题考查等可能事件的概率,考查利用分类计数原理表示事件数,考查理解能力和运算能力,本题解题的关键是注意列举出的事件数做到不重不漏.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
19.根据定积分的定义,${∫}_{0}^{2}$x2dx等于( )
| A. | $\sum_{i=1}^{n}$($\frac{i-1}{n}$)2•$\frac{1}{n}$ | B. | $\underset{lim}{n→∞}$$\sum_{i=1}^{n}$($\frac{i-1}{n}$)2•$\frac{1}{n}$ | ||
| C. | $\sum_{i=1}^{n}$($\frac{2i}{n}$)2•$\frac{2}{n}$ | D. | $\underset{lim}{n→∞}$$\sum_{i=1}^{n}$($\frac{2i}{n}$)2•$\frac{2}{n}$ |
12.“$α=\frac{π}{2}$”是“cos2α=-1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.两个不同的平面α、β,m为α内的一条直线,命题p:α⊥β,命题q:m⊥β,则p是q的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
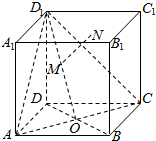 如图所示,正方体ABCD-A1B1C1D1的棱长为1,BD∩AC=O,M是线段D1O上的动点,过点M作平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为$\frac{\sqrt{6}}{2}$.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,BD∩AC=O,M是线段D1O上的动点,过点M作平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为$\frac{\sqrt{6}}{2}$.