题目内容
若函数f(2x)=log3(x+1),则f(4)= .
考点:函数的值
专题:函数的性质及应用
分析:直接利用函数的解析式,求解函数值即可.
解答:
解:函数f(2x)=log3(x+1),
则f(4)=f(2×2)=log33=1.
故答案为:1.
则f(4)=f(2×2)=log33=1.
故答案为:1.
点评:本题考查函数的值的求法,函数的解析式的应用.

练习册系列答案
相关题目
设集合A={2,4,5,7},B={3,4,5},则A∩B=( )
| A、{4,5} |
| B、{2,3,4,5,7} |
| C、{2,7} |
| D、{3,4,5,6,7} |
已知{an},{bn}均为等差数列,且a2=8,a6=16,b2=4,b6=a6,则由{an},{bn}的公共项组成的新数列{cn}的通项公式cn等于( )
| A、3n+4 | B、6n+2 |
| C、6n+4 | D、2n+2 |
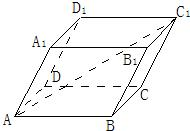 如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.
如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.