题目内容
己知双曲线C：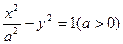
与直线l：x + y = 1相交于两个不同的点A、B
(I) 求双曲线C的离心率e的取值范围；
(Ⅱ) 设直线l与y轴交点为P，且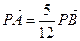
，求
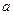的值。
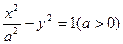与直线l：x + y = 1相交于两个不同的点A、B(I) 求双曲线C的离心率e的取值范围；
(Ⅱ) 设直线l与y轴交点为P，且
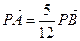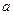，求的值。
，
解：（Ⅰ）由曲线C与直线相交于两个不同的点，知方程组
有两个不同的解，消去Y并整理得：
①……………2分
双曲线的离心率
……………………………………5分∵
∴…………………………………6分即离心率e的取值范围为
．…………………………7分（Ⅱ）设
.m∵
,∴
，得
…………9分由于
是方程①的两个根，∴
即
，得
，………………………………………………………………12分解得
。…………………………………………………………………14分
练习册系列答案
相关题目
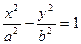(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥
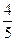c.求双曲线的离心率e的取值范围
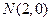并且与圆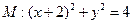
相外切，动圆圆心P的轨迹为W，过点N的直线
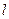与轨迹W交于A、B两点。
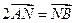，求直线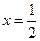
上是否存在一点Q，使得
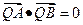，并说明理由。
，则双曲线的离心率为 ．
为双曲线
右支上除顶点外任一点，
为双曲线的左右顶点，直线
的分别斜率为
，则
。
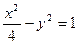的焦点坐标为（ ﹡ ）．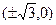 
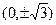
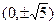
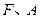分别为双曲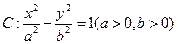
的左焦点、右顶点，点
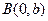满足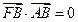
，则双曲线的离心率为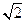
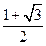
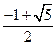
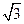
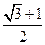
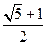
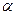是第四象限角，则方程
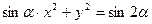所表示的曲线是（ ）
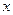轴上的椭圆；
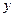轴上的椭圆；