题目内容
14.若0<α<2π且cosα≤$\frac{1}{2}$,sinα>$\frac{\sqrt{2}}{2}$,则角α的取值范围是( )| A. | [$\frac{π}{3}$,$\frac{3}{4}$π) | B. | ($\frac{π}{3}$,$\frac{3}{4}$π] | C. | ($\frac{π}{4}$,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{3}{4}$π)∪($\frac{π}{4}$,$\frac{π}{3}$) |
分析 运用余弦函数在(0,2π)的图象,求得cosα≤$\frac{1}{2}$,再由正弦函数在(0,2π)的图象,求得sinα>$\frac{\sqrt{2}}{2}$,求交集,即可得到所求范围.
解答 解:由0<α<2π且cosα≤$\frac{1}{2}$,
可得$\frac{π}{3}$≤α≤$\frac{5π}{3}$①,
sinα>$\frac{\sqrt{2}}{2}$,可得$\frac{π}{4}$<α<$\frac{3π}{4}$②.
由①②可得$\frac{π}{3}$≤α<$\frac{3π}{4}$.
故选:A.
点评 本题考查三角函数的图象和性质,主要考查正弦函数和余弦函数的图象,考查运算能力,属于基础题.

练习册系列答案
相关题目
14.下列结构图中要素之间表示从属关系的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
5.已知等差数列{an}前9项和为27,a10=8,则a99=( )
| A. | 100 | B. | 99 | C. | 98 | D. | 97 |
3.曲线$y=cosx(-\frac{π}{2}<x<π)$与x轴围成的面积是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
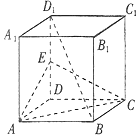 如图,正方体 A BCD-A1 B1C1D1中,E为DD1的中点.
如图,正方体 A BCD-A1 B1C1D1中,E为DD1的中点.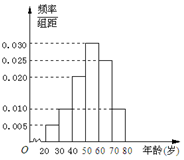 广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.