题目内容
若f(x+1)的定义域为(-
,2),求f(x2)的定义域.
| 1 |
| 2 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据f(x+1)的定义域即x的取值范围,求出x+1的取值范围,即x2的取值范围,再求出x的取值范围,即f(x2)的定义域.
解答:
解:∵f(x+1)的定义域为(-
,2),
∴x∈(-
,2),
∴x+1∈(
,3);
令x2∈(
,3),
∴x∈(-
,-
)∪(
,
);
∴f(x2)的定义域为(-
,-
)∪(
,
).
| 1 |
| 2 |
∴x∈(-
| 1 |
| 2 |
∴x+1∈(
| 1 |
| 2 |
令x2∈(
| 1 |
| 2 |
∴x∈(-
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
∴f(x2)的定义域为(-
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
点评:本题考查了求函数的定义域的问题,解题时应明确函数的定义域是自变量的取值范围,是基础题.

练习册系列答案
相关题目
已知向量
=(-a,2,1)与
=(1,2a,-3)垂直,则a等于( )
| m |
| n |
| A、2 | B、-2 | C、1 | D、-1 |
空间中,对于平面α和共面的两直线m、n,下列命题中为真命题的是( )
| A、若m⊥α,m⊥n,则n∥α |
| B、若m∥α,n∥α,则m∥n |
| C、若m、n与α所成的角相等,则m∥n |
| D、若m?α,n∥α,则m∥n |
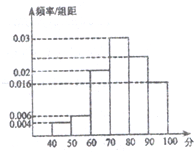 从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.
从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.