题目内容
已知函数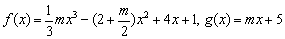 .
.
(1)当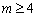 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)是否存在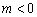 ,使得对任意的
,使得对任意的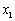 ,
,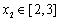 都有
都有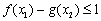 ,若存在,求
,若存在,求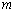 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
.解:(1)
 .
.
i) 若 时,则
时,则 ,
,
此时 都有
都有 ,
,  有
有 .
.
 的单调递增区间为
的单调递增区间为 和
和 .
.
ii)若 ,则
,则 ,
,
 的单调递增区间为
的单调递增区间为 .
.
(2)当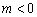 时,
时,
 且
且 ,
,
 当
当 时,都有
时,都有 .
.
 此时,
此时, 在
在 上单调递减
上单调递减  ...又
...又 在
在 上单调递减.
上单调递减. .
.
由已知
解得 又
又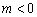 .
. .
.
综上所述,存在 使对任意
使对任意 ,都有
,都有 成立
成立

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 左焦点
左焦点 且垂直于双曲线一渐近线的直线与双
且垂直于双曲线一渐近线的直线与双  ,
, 为原点,若
为原点,若 ,则
,则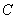 的离心率为 ( )
的离心率为 ( ) B.
B. C.
C.  D.
D.
 ,
,
 的周期和最大值(Ⅱ)求
的周期和最大值(Ⅱ)求 ”是“一元二次方程
”是“一元二次方程 ”有实数解的
”有实数解的 的图象关于直线
的图象关于直线 对称,且当
对称,且当 成立若a=(20.2)·
成立若a=(20.2)· ·
· ·
· ,则a,b,c的大小关系是
,则a,b,c的大小关系是  B.
B. C.
C. D.
D.
 的图象可能是
的图象可能是 
 的零点个数是
的零点个数是