题目内容
如图:二面角 的大小是
的大小是 ,线段
,线段 与
与 所成角为
所成角为 ,则
,则 与平面
与平面 所成角的正弦值是_________ .
所成角的正弦值是_________ . 

解析试题分析:过点A作平面β的垂线,垂足为C,
在β内过C作l的垂线.垂足为D
连接AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角α-l-β的平面角,为60°
又由已知,∠ABD=45°
连接CB,则∠ABC为AB与平面β所成的角,设AD=2,则AC=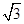 ,CD=1,AB=AD:sin450=2
,CD=1,AB=AD:sin450=2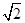 ,∴sin∠ABC=AC:AB=
,∴sin∠ABC=AC:AB= ;故答案为
;故答案为 .
.
考点:本题主要是考查平面与平面之间的位置关系,以及直线与平面所成角,考查空间想象能力、运算能力和推理论证能力,属于基础题.
点评:解决该试题的关键是过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D,连接AD,从而∠ADC为二面角α-l-β的平面角,连接CB,则∠ABC为AB与平面β所成的角,在直角三角形ABC中求出此角即可.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
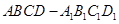 ,底面
,底面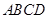 是正方形,
是正方形,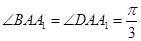 ,则棱
,则棱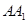 和底面所成角为 。
和底面所成角为 。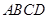 -
- 中,
中,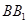 与平面
与平面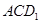 所成角的余弦值为 .
所成角的余弦值为 .  =
= ,则点
,则点 与直线
与直线 的位置关系用符号表示为 ;
的位置关系用符号表示为 ; ,其中m∥n,那么在平面
,其中m∥n,那么在平面 中,平面
中,平面 和平面
和平面 的位置关系为
的位置关系为