题目内容
18.若直线y=2x+b与椭圆$\frac{{x}^{2}}{4}$+y2=1无公共点,则b的取值范围为b$<-2\sqrt{2}$或b$>2\sqrt{2}$.分析 联立直线与椭圆方程,通过判别式小于0 求解即可.
解答 解:由题意可得:$\left\{\begin{array}{l}{y=2x+b}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得:8x2+4bx+b2-4=0,
直线y=2x+b与椭圆$\frac{{x}^{2}}{4}$+y2=1无公共点,
所以:△=16b2-32(b2-4)<0,
-b2+8<0,解得b$<-2\sqrt{2}$或b$>2\sqrt{2}$.
故答案为:b$<-2\sqrt{2}$或b$>2\sqrt{2}$.
点评 本题考查直线与椭圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
9.一个圆锥的侧面展开图是一个$\frac{1}{4}$的圆面,则这个圆锥的表面积和侧面积的比是( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{6}{5}$ |
13.下列对应f是集合A到集合B的函数的是( )
| A. | A={-1,0,1},B={0,1},f:A中的数平方 | B. | A={0,1},B={-1,0,1},f:A中的数开方 | ||
| C. | A=Z,B=Q,f:A中的数取倒数 | D. | A=R,B={正实数},f:A中的数取绝对值 |
8.设椭圆$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1,则该椭圆的焦点坐标为( )
| A. | (-$\sqrt{5}$,0),($\sqrt{5}$,0) | B. | (0,-$\sqrt{5}$),(0,$\sqrt{5}$) | C. | (-$\sqrt{13}$,0),($\sqrt{13}$,0) | D. | (0,-$\sqrt{13}$),(0,$\sqrt{13}$) |
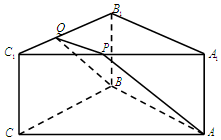 如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).