题目内容
7.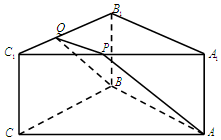 如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).(Ⅰ)证明:PQ∥A1B1;
(Ⅱ)当CF⊥平面ABQP时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四面体CABF的体积.
分析 (I)利用面面平行的性质定理即可证明.
(II)F点是PQ中点,理由如下:当$λ=\frac{1}{2}时$,P、Q分别是A1C1,A1B1的中点,连接CQ和CP,由ABC-A1B1C1是正三棱柱,可得CQ=CP,CF⊥QP,取AB中点H,连接FH,CH,在等腰梯形ABQP中,FH2=AP2-$\frac{1}{4}A{B}^{2}$,可得CF2+FH2=CH2,可得CF⊥FH.可得CF⊥平面ABF,即CF⊥平面ABQP,即可得出.
解答 (I)证明:∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,
又∵AB∥A1B1,∴PQ∥A1B1.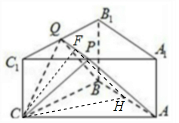
(Ⅱ)解:F点是PQ中点,理由如下:
当$λ=\frac{1}{2}时$,P、Q分别是A1C1,A1B1的中点,连接CQ和CP,
∵ABC-A1B1C1是正三棱柱,∴CQ=CP,∴CF⊥QP,
取AB中点H,连接FH,CH,在等腰梯形ABQP中,
FH2=AP2-$\frac{1}{4}A{B}^{2}$=$\frac{3}{2}$.
CF=$\frac{{\sqrt{6}}}{2}$,CH=$\sqrt{3}$,
∴CF2+FH2=CH2,∴CF⊥FH,
∵QP∩FH=H,∴CF⊥平面ABF,即CF⊥平面ABQP,
∴F点是C在平面ABQP内的正投影.
∴${V_{C-ABF}}=\frac{1}{3}×\frac{1}{2}•2•\frac{{\sqrt{6}}}{2}×\frac{{\sqrt{6}}}{2}=\frac{1}{2}$.
点评 本题考查了正三棱柱的性质、线面平行垂直的判定与性质定理、等腰梯形等腰三角形的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $(-∞,\sqrt{e})$ | B. | (-e,e) | C. | $(-\frac{1}{e},\sqrt{e})$ | D. | (-∞,e) |