Question

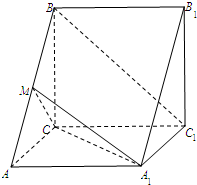
如图，已知正三棱柱ABC-A₁B₁C₁的各条棱长都相等，则异面直线AB₁和A₁C所成的角的余弦值大小是______．

Answer 1

延长CA到D，使得AD=AC，则ADA₁B₁为平行四边形，
∴AB₁∥A₁D，
∴∠DA₁C就是异面直线AB₁和A₁C所成的角，
又三角形ABC为等边三角形，设AB=AA₁=1，∠CAD=120°
则CD=

1+1-2×1×1×(- 1 2 )

=

3

；A₁C=A₁D=

2

，
在△A₁CD中，cos∠DA₁C=

2+2-3

2× 2 × 2

=

1

4

．
故答案是：

1

4

．