题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若对任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)当
(2)当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() ;
;
(3)![]()
【解析】
(1)![]() ,
,![]() ,
,![]() ,方程易求;
,方程易求;
(2)![]() ,根据
,根据![]()
![]() 的正负分类讨论
的正负分类讨论![]() 的单调性即可;
的单调性即可;
(3)对任意的![]() ,使
,使![]() 成立,只需任意的
成立,只需任意的![]() ,
,![]() ,以下分
,以下分![]() 、
、![]() 、
、![]() 三种情况讨论
三种情况讨论
解:(1)![]() 时,
时,![]() ,
,![]()
![]() ,
,![]()
∴![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
故答案为:![]() ;
;
(2)![]()
①当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 的递增区间为
的递增区间为![]()
②当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]()
|
|
|
|
| - | + | |
| 减 | 增 |
所以函数![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]()
当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 的递增区间为
的递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() .
.
(3)对任意的![]() ,使
,使![]() 成立,只需任意的
成立,只需任意的![]() ,
,![]()
①当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
所以只需![]()
而![]()
所以![]() 满足题意;
满足题意;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
所以只需![]()
而![]() ,
,
所以![]() 满足题意;
满足题意;
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,![]() 上是增函数,
上是增函数,
所以只需![]() 即可
即可
而![]()
从而![]() 不满足题意;
不满足题意;
综合①②③实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资![]() (单位:元)与月销售产品件数
(单位:元)与月销售产品件数![]() 的函数关系式;
的函数关系式;
(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某个餐厅打算从上表的6种等级的中国小龙虾中随机选2种进行促销,记被选中的2种等级代码数值在60以下(不含60)的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:对一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: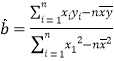 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.