题目内容
【题目】如图，设
，
分别是正方体
的棱
上两点，且
，
，其中正确的命题为（ ）
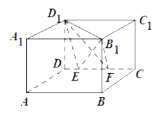
A.三棱锥
的体积为定值
B.异面直线
与
所成的角为
C.
平面
D.直线与平面所成的角为
【答案】AD
【解析】
A. 利用
，三棱锥
的体积为定值，正确
B. 利用平移法找异面直线所成的角，
，
和
所成的角为
，所以异面直线与
所成的角为，故B错误
C. 若
平面
，则线与所成的角为
，而异面直线与所成的角为，故C错误
D，建立坐标系，用向量坐标法求解，先求出平面的一个法向量，再求平面的一个法向量和的方向向量的夹角，正确
解：对于A，
故三棱锥的体积为定值，故A正确
对于B， ，和所成的角为，异面直线与所成的角为，故B错误
对于C， 若平面，则直线，即异面直线与所成的角为，故C错误
对于D，以
为坐标原点，分布以
为
轴，
轴，
轴，建立空间直角坐标系，设
，则
，
，
设平面的法向量为
则
，即
令
，则
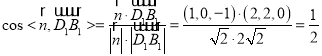
所以直线与平面所成的角为
，正确
故选：AD
练习册系列答案
相关题目
