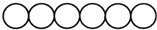题目内容
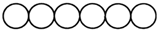用红黄蓝三种颜色给如图所示的六连圆涂色，若每种颜色只能涂两个圆，且相邻两个圆所涂颜色不能相同，则不同的涂色方案共有
- A.18 个
- B.24 个
- C.30 个
- D.36 个
C
分析：先涂前三个圆，再涂后三个圆．若涂前三个圆用3种颜色，求出不同的涂法种数．若涂前三个圆用2种颜色，再求出涂法种数，把这两类涂法的种数相加，即得所求．
解答：先涂前三个圆，再涂后三个圆．
若涂前三个圆用3种颜色，有
=6种方法；则涂后三个圆也用3种颜色，有
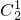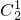•=4种方法，
此时，故不同的涂法有6×4=24种．
若涂前三个圆用2种颜色，则涂后三个圆也用2种颜色，共有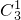
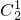•=6种方法．
综上可得，所有的涂法共有24+6=30 种，
故选C．
点评：本题考查排列、组合及简单计数问题，体现了分类讨论的数学思想，属于中档题．
分析：先涂前三个圆，再涂后三个圆．若涂前三个圆用3种颜色，求出不同的涂法种数．若涂前三个圆用2种颜色，再求出涂法种数，把这两类涂法的种数相加，即得所求．
解答：先涂前三个圆，再涂后三个圆．
若涂前三个圆用3种颜色，有
=6种方法；则涂后三个圆也用3种颜色，有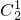•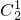=4种方法，此时，故不同的涂法有6×4=24种．
若涂前三个圆用2种颜色，则涂后三个圆也用2种颜色，共有
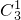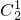•=6种方法．综上可得，所有的涂法共有24+6=30 种，
故选C．
点评：本题考查排列、组合及简单计数问题，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目
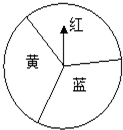如图一个圆盘被三等分，分别涂上红黄蓝三种颜色，小明和小亮用的这一个转盘进行“配紫色”游戏．游戏规则如下：每次任意转动转盘，再等转盘停止时，指针指向哪种颜色，结果就记为这种颜色，连续转动两次转盘，如果两次转盘转出的颜色相同或配成紫色（若其中一次转盘转出蓝色，另一次转出红色，则可配成紫色），则小明得1分，否则小亮得1分．试问：
（2006•崇文区二模）如图，用红、黄、绿、橙、蓝五种颜色给图中的三个方格涂色，每格涂一种颜色，相邻格涂不同颜色，问共有
（2012•温州二模）用红黄蓝三种颜色给如图所示的六连圆涂色，若每种颜色只能涂两个圆，且相邻两个圆所涂颜色不能相同，则不同的涂色方案共有（ ）