题目内容
已知直线y=kx-1与双曲线x2-y2=1的左支交于不同两点A、B,若另有一条直线l经过P(-2,0)及线段AB的中点Q.(1)求k的取值范围;
(2)求直线l在y轴上的截距b的取值范围.
【答案】分析:(1)由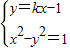 ,得(1-k2)x2+2kx-2=0.再由直线y=kx-1与双曲线x2-y2=1的左支交于不同两点A、B,利用根的判别式和韦达定理能求出k的取值范围.
,得(1-k2)x2+2kx-2=0.再由直线y=kx-1与双曲线x2-y2=1的左支交于不同两点A、B,利用根的判别式和韦达定理能求出k的取值范围.
(2)由直线l经过P(-2,0)及线段AB的中点Q,知直线l的方程为得x-(2k2+k-2)y+2=0,令x=0,解得直线l在y轴上的截距b=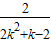 .设f(k)=2k2+k-2=2(k+
.设f(k)=2k2+k-2=2(k+ )2-
)2-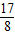 ,由此能求出直线l在y轴上的截距b的取值范围.
,由此能求出直线l在y轴上的截距b的取值范围.
解答:(本小题满分12分)
解:(1)由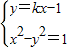 ,得(1-k2)x2+2kx-2=0.
,得(1-k2)x2+2kx-2=0.
直线y=kx-1与双曲线x2-y2=1的左支交于不同两点A、B,
∴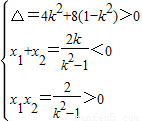 ,解得-
,解得-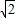 <k<-1.
<k<-1.
∴k的取值范围是(-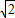 ,-1).(6分)
,-1).(6分)
(2)∵直线l经过P(-2,0)及线段AB的中点Q,
设Q(x,y),∴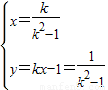 ,
,
∴直线l的方程为: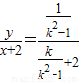 ,整理,得x-(2k2+k-2)y+2=0,
,整理,得x-(2k2+k-2)y+2=0,
令x=0,解得直线l在y轴上的截距b=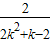 .
.
设f(k)=2k2+k-2=2(k+ )2-
)2-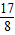 ,
,
则f(k)在(-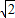 ,-1)上是减函数,
,-1)上是减函数,
∴f(-1)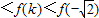 ,且f(k)≠0,
,且f(k)≠0,
∴-1<f(k)<2-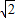 ,且f(k)≠0,
,且f(k)≠0,
∴b<-2,或b>2+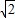 ,
,
故直线l在y轴上的截距b的取值范围是(-∞,-2)∪(2+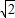 ,+∞)…12分
,+∞)…12分
点评:本题考查直线的斜率的取值范围的求法,考查直线纵截距的取值范围的求法.解题时要认真审题,注意构造法的合理运用.
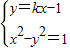 ,得(1-k2)x2+2kx-2=0.再由直线y=kx-1与双曲线x2-y2=1的左支交于不同两点A、B,利用根的判别式和韦达定理能求出k的取值范围.
,得(1-k2)x2+2kx-2=0.再由直线y=kx-1与双曲线x2-y2=1的左支交于不同两点A、B,利用根的判别式和韦达定理能求出k的取值范围.(2)由直线l经过P(-2,0)及线段AB的中点Q,知直线l的方程为得x-(2k2+k-2)y+2=0,令x=0,解得直线l在y轴上的截距b=
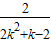 .设f(k)=2k2+k-2=2(k+
.设f(k)=2k2+k-2=2(k+ )2-
)2-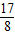 ,由此能求出直线l在y轴上的截距b的取值范围.
,由此能求出直线l在y轴上的截距b的取值范围.解答:(本小题满分12分)
解:(1)由
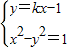 ,得(1-k2)x2+2kx-2=0.
,得(1-k2)x2+2kx-2=0.直线y=kx-1与双曲线x2-y2=1的左支交于不同两点A、B,
∴
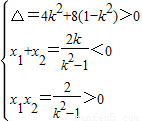 ,解得-
,解得-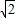 <k<-1.
<k<-1.∴k的取值范围是(-
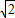 ,-1).(6分)
,-1).(6分)(2)∵直线l经过P(-2,0)及线段AB的中点Q,
设Q(x,y),∴
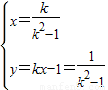 ,
,∴直线l的方程为:
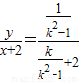 ,整理,得x-(2k2+k-2)y+2=0,
,整理,得x-(2k2+k-2)y+2=0,令x=0,解得直线l在y轴上的截距b=
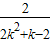 .
.设f(k)=2k2+k-2=2(k+
 )2-
)2-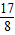 ,
,则f(k)在(-
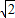 ,-1)上是减函数,
,-1)上是减函数,∴f(-1)
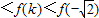 ,且f(k)≠0,
,且f(k)≠0,∴-1<f(k)<2-
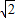 ,且f(k)≠0,
,且f(k)≠0,∴b<-2,或b>2+
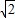 ,
,故直线l在y轴上的截距b的取值范围是(-∞,-2)∪(2+
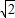 ,+∞)…12分
,+∞)…12分点评:本题考查直线的斜率的取值范围的求法,考查直线纵截距的取值范围的求法.解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
(理)已知直线y=kx+1(k∈R)与椭圆
+
=1总有交点,则m的取值范围为( )
| x2 |
| 2 |
| y2 |
| m |
| A、(1,2] |
| B、[1,2) |
| C、[1,2)∪[2,+∞) |
| D、(2,+∞) |