题目内容
（理）已知直线y=kx+1（k∈R）与椭圆
+
=1总有交点，则m的取值范围为（ ）
| x2 |
| 2 |
| y2 |
| m |
| A、（1，2] |
| B、[1，2） |
| C、[1，2）∪[2，+∞） |
| D、（2，+∞） |
分析：根据直线y=kx+1（k∈R）与椭圆
+
=1总有交点，直线过定点（0，1），只需保证（0，1）在椭圆上或椭圆内部即可，即
≤1
| x2 |
| 2 |
| y2 |
| m |
| 1 |
| m |
解答：解：直线y=kx+1过定点（0，1），若椭圆
+
=1与直线y=kx+1恒有交点，只需要保证点（0，1）在椭圆上或在椭圆内部，所以
≤1，即m≥1．
又
+
=1为椭圆，所以m＞0且m≠2．从而m的取值范围是[1，2）∪[2，+∞）
故选C．
| x2 |
| 2 |
| y2 |
| m |
| 1 |
| m |
又
| x2 |
| 2 |
| y2 |
| m |
故选C．
点评：本题考查了直线与椭圆的关系，属于常见题型．
练习册系列答案
相关题目
)的图象(如图所示)有且仅有两个公共点,若这两个公共点的横坐标分别为α、β,且β＜α,则下列结论中正确的是
)=β B.tan(β-
)=α C.tan(α-
)=α D.tan(β-
)=β
+
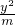=1总有交点，则m的取值范围为
+
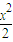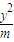=1总有交点，则m的取值范围为（ ）
+
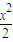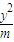=1总有交点，则m的取值范围为（ ）