题目内容
设f(x)=
(1)求f(x)的值域;
(2)判断F(x)=lgf(x)在[-1,1]上的单调性,并说明理由;
(3)求证:lg
≤F(|t-
|-|t+
|)≤lg
(t∈R).
| 2x2-2x+2 |
| x2+1 |
(1)求f(x)的值域;
(2)判断F(x)=lgf(x)在[-1,1]上的单调性,并说明理由;
(3)求证:lg
| 7 |
| 5 |
| 1 |
| 6 |
| 1 |
| 6 |
| 13 |
| 5 |
考点:函数单调性的判断与证明,函数的值域
专题:函数的性质及应用,导数的综合应用
分析:(1)设y=
,将该式整理成关于x的方程,根据方程有解即可求得函数f(x)的值域;
(2)求F′(x),然后判断F′(x)的符号,从而判断出函数F(x)在[-1,1]上单调递减;
(3)根据数轴上两点间的距离的表示可以知道|t-
|-|t+
|表示数轴上到点
,与到-
距离的差,所以便得到-
≤|t-
|-|t+
|≤
,从而根据F(x)在[-1,1]上单调递减即可证得该问.
| 2x2-2x+2 |
| x2+1 |
(2)求F′(x),然后判断F′(x)的符号,从而判断出函数F(x)在[-1,1]上单调递减;
(3)根据数轴上两点间的距离的表示可以知道|t-
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
解答:
解:(1)设y=
,由该函数得:y(x2+1)=2x2-2x+2,整理成:
(2-y)x2-2x+2-y=0,关于x的方程有解;
∴若y=2,则方程变成-2x=0,x=0,即方程有解;
若y≠2,则:△=4-4(2-y)2≥0,解得:1≤y≤3;
∴函数f(x)的值域为[1,3];
(2)F′(x)=
;
∵2x2-2x+2=2(x-
)2+
>0,x∈[-1,1];
∴x2-1≤0;
∴F′(x)≤0;
∴F(x)在[-1,1]上单调递减;
(3)证明:|t-
|-|t+
|=|t-
|-|t-(-
)|;
∴|t-
|-|t+
|表示数轴上到
的距离与到-
距离的差;
∴-
≤|t-
|-|t+
|≤
;
∵F(x)在[-1,1]上单调递减;
∴F(
)≤F(|t-
|-|t+
|)≤F(-
);
又F(
)=lg
,F(-
)=lg
;
∴lg
≤F(|t-
|-|t+
|)≤lg
.
| 2x2-2x+2 |
| x2+1 |
(2-y)x2-2x+2-y=0,关于x的方程有解;
∴若y=2,则方程变成-2x=0,x=0,即方程有解;
若y≠2,则:△=4-4(2-y)2≥0,解得:1≤y≤3;
∴函数f(x)的值域为[1,3];
(2)F′(x)=
| 2(x2+1)(x2-1) |
| 2x2-2x+2 |
∵2x2-2x+2=2(x-
| 1 |
| 2 |
| 3 |
| 2 |
∴x2-1≤0;
∴F′(x)≤0;
∴F(x)在[-1,1]上单调递减;
(3)证明:|t-
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
∴|t-
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
∴-
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
∵F(x)在[-1,1]上单调递减;
∴F(
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
又F(
| 1 |
| 3 |
| 7 |
| 5 |
| 1 |
| 3 |
| 13 |
| 5 |
∴lg
| 7 |
| 5 |
| 1 |
| 6 |
| 1 |
| 6 |
| 13 |
| 5 |
点评:考查该题求值域的方法:将函数变成关于x的方程,根据方程有解求值域,根据函数导数符号判断函数单调性的方法,数轴上两点间距离的表示.

练习册系列答案
相关题目
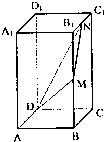 如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )
如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )| A、圆或圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、椭圆的一部分 |
若椭圆2kx2+ky2=1的一个焦点坐标是(0,4),则k的值为( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
下列命题不正确的是( )
A、如果f(x)=
| |||||||
B、如果f(n)=
| |||||||
C、如果f(x)=2x-1,则
| |||||||
D、如果f(x)=
|