题目内容
17.若函数f(x)=$\frac{{x}^{3}}{3}$-$\frac{a}{2}$x2+x+1在区间($\frac{1}{3}$,4)上有极值点,则实数a的取值范围是(2,$\frac{17}{4}$).分析 求导f′(x);得到f′(x)=0,($\frac{1}{3}$,4)有解即可.
解答 解:∵f(x)=$\frac{{x}^{3}}{3}$-$\frac{a}{2}$x2+x+1,
∴f′(x)=x2-ax+1,
∴x2-ax+1=0有两个解,
则△=a2-4>0;
故a>2或a<-2;
函数f(x)=$\frac{{x}^{3}}{3}$-$\frac{a}{2}$x2+x+1在区间($\frac{1}{3}$,4)上有极值点可化为x2-ax+1=0在区间($\frac{1}{3}$,4)有解,
①若x2-ax+1=0在区间($\frac{1}{3}$,4)有两个解,
则满足f′($\frac{1}{3}$)>0且f′(4)>0,
即$\frac{1}{9}$-$\frac{1}{3}$a+1>0且16-4a+1>0,
故a<$\frac{10}{3}$且a<$\frac{17}{4}$;
故2<a<$\frac{10}{3}$;
②若x2-ax+1=0在区间($\frac{1}{3}$,4)内只有1个解,
则满足f′($\frac{1}{3}$)f′(4)<0,
即($\frac{1}{9}$-$\frac{1}{3}$a+1)(16-4a+1)<0,
即($\frac{10}{9}$-$\frac{1}{3}$a)(17-4a)<0,
则(a-$\frac{10}{3}$)(a-$\frac{17}{4}$)<0,
则$\frac{10}{3}$<a<$\frac{17}{4}$;
当a=$\frac{10}{3}$时,f′(x)=x2-$\frac{10}{3}$x+1=$\frac{1}{3}$(x-3)(3x-1),
由f′(x)=0得x=3或x=$\frac{1}{3}$,
此时当x=$\frac{1}{3}$时,函数f(x)取得极值,
综上所述,2<a<$\frac{17}{4}$.
故答案为:(2,$\frac{17}{4}$)
点评 本题主要考查导数的应用,利用函数极值和导数的关系进行求解是解决本题的关键.注意要进行分类讨论.

| A. | 1≤m≤2 | B. | $\frac{1}{2}$≤m≤2 | C. | -$\frac{1}{2}$≤m≤2 | D. | -2≤m≤1 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | -2 | B. | 0 | C. | 5 | D. | 10 |
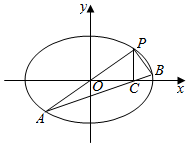 如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.
如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.