题目内容
11．已知复数z的共轭复数为$\overline{z}$，若（$\frac{3z}{2}$+$\frac{\overline{z}}{2}$）（1-2$\sqrt{2}$i）=5-$\sqrt{2}$i（i为虚数单位），则在复平面内，复数z所对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 设z=a+bi（a，b∈R），代入（$\frac{3z}{2}$+$\frac{\overline{z}}{2}$）（1-2$\sqrt{2}$i）=5-$\sqrt{2}$i，利用复数代数形式的乘除运算化简后利用复数相等的条件列式求得a，b的值得答案．
解答 解：设z=a+bi（a，b∈R），
则由（$\frac{3z}{2}$+$\frac{\overline{z}}{2}$）（1-2$\sqrt{2}$i）=5-$\sqrt{2}$i，得
$\frac{3（a+bi）+a-bi}{2}×（1-2\sqrt{2}i）=5-\sqrt{2}i$，
即$（2a+2\sqrt{2}b）+（b-4\sqrt{2}a）i=5-\sqrt{2}i$，
得$\left\{\begin{array}{l}{2a+2\sqrt{2}b=5}\\{4\sqrt{2}a-b=\sqrt{2}}\end{array}\right.$，解得a=$\frac{1}{2}$，b=$\sqrt{2}$．
∴在复平面内，复数z所对应的点的坐标为（$\frac{1}{2}，\sqrt{2}$），位于第一象限．
故选：A．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
19．在数列{an}中，a1=1，an+1=2an，${S_n}=a_1^2-a_2^2+a_3^2-a_4^2+$…$+a_{2n-1}^2-a_{2n}^2$等于（ ）
| A． | $\frac{1}{3}（{2^n}-1）$ | B． | $\frac{1}{5}（1-{2^{4n}}）$ | C． | $\frac{1}{3}（{4^n}-1）$ | D． | $\frac{1}{3}（1-{2^n}）$ |
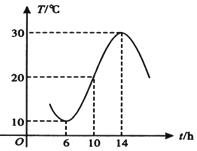如图所示，某地一天6～14时的温度变化曲线近似满足函数y=Asin（ωx+ϕ）+b（|ϕ|＜π），则这段曲线的函数解析式可以为y=10sin（$\frac{π}{8}x+\frac{3π}{4}$）+20；（6≤x≤14）．
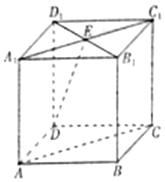如图所示，在正方体AC1中，AB=2，A1C1∩B1D1=E，直线AC与直线DE所成的角为α，直线DE与平面BCC1B1所成的角为β，则cos（α-β）=$\frac{\sqrt{6}}{6}$．
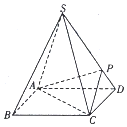如图，四棱锥S-ABCD的底面边长为1的正方形，每条侧棱的长均为$\sqrt{2}$，P为侧棱SD上的点．