题目内容
19.为了解某地区某种农产品的年产量x(单位:万吨)对价格y(单位:千元/吨)和年利润z的影响,对近五年该农产品的年产量和价格统计如下表:| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
分析 (Ⅰ)由表中的数据分别计算,即可写出线性回归方程;
(Ⅱ)由线性回归方程,计算x=10时,的值即可.
解答 解:(1)由表中的数据得$\overline{x}$=30000,$\overline{y}$=5,$\sum_{i=1}^{5}$xiyi=627000,$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=5500000000
∴b=$\frac{627000-5×30000×5}{5500000000-5×900000000}$≈-0.000123
∴a=5-0.000123×30000=1.31,
∴所求线性回归方程为y=-0.000123x+1.31;
(2)由(1)得,z=x(y-2)=x(-0.000123x-0.69),无解.
点评 本题考查了求线性回归方程的应用问题,也考查了利用线性回归方程预测生产问题,是基础题目.

练习册系列答案
相关题目
9.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2014}$的值的一个程序框图,则判断框内可填入的条件是( )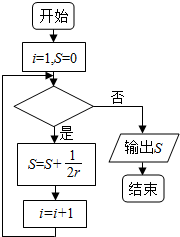

| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |
8.若x∈(1,a),则M=logax2,N=loga2x的大小关系是( )
| A. | M<N | B. | M>N | C. | M=N | D. | 不能确定 |
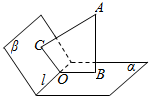 如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度.
如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度. 如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.
如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.