题目内容
14.在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆O:x2+y2=r2(0<r<b).当圆O的一条切线l:y=kx+m与椭圆E相交于A,B两点.(Ⅰ)当k=-$\frac{1}{2}$,r=1时,若点A,B都在坐标轴的正半轴上,求椭圆E的方程;
(Ⅱ)若以AB为直径的圆经过坐标原点O,探究a,b,r是否满足$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{r}^{2}}$,并说明理由.
分析 (Ⅰ)利用点到直线的距离公式求得d=$\frac{丨-2m丨}{\sqrt{{2}^{2}+{1}^{2}}}$=1,即可求得m的值,由点A,B都在坐标轴的正半轴上,即可求得a和b的值,求得椭圆方程;
(Ⅱ)利用点到直线的距离公式,求得m2=r2(1+k2),将直线方程代入椭圆方程,由韦达定理及向量数量积的坐标运算x1x2+y1y2=0,即可求得a,b与r的关系.
解答 解:(Ⅰ)当k=-$\frac{1}{2}$,r=1时,则切线l:y=-$\frac{1}{2}$x+m,即2y+x-2m=0,
由圆心到l的距离d=$\frac{丨-2m丨}{\sqrt{{2}^{2}+{1}^{2}}}$=1,解得:m=±$\frac{\sqrt{5}}{2}$,
点A,B都在坐标轴的正半轴上,则m>0,
∴直线l:y=-$\frac{1}{2}$x+$\frac{\sqrt{5}}{2}$,
∴A(0,$\frac{\sqrt{5}}{2}$),B($\sqrt{5}$,0),
∴B为椭圆的右顶点,A为椭圆的上顶点,
则a=$\sqrt{5}$,b=$\frac{\sqrt{5}}{2}$,
∴椭圆方程为:$\frac{{x}^{2}}{5}+\frac{4{y}^{2}}{5}=1$;
(Ⅱ)a,b,r满足$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{r}^{2}}$成立,
理由如下:设点A、B的坐标分别为A(x1,y1)、B(x2,y2),
直线l与圆x2+y2=r2相切,
则$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$=r,即m2=r2(1+k2),①
则$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0.
则x1+x2=-$\frac{2{a}^{2}km}{{b}^{2}+{a}^{2}{k}^{2}}$,x1x2=$\frac{{a}^{2}{m}^{2}-{a}^{2}{b}^{2}}{{b}^{2}+{a}^{2}{b}^{2}}$,
所以y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=$\frac{{b}^{2}{m}^{2}-{a}^{2}{b}^{2}{k}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$,
AB为直径的圆经过坐标原点O,则∠AOB=90°,则$\overrightarrow{OA}$⊥$\overrightarrow{OB}$=0,
∴x1x2+y1y2=$\frac{{a}^{2}{m}^{2}-{a}^{2}{b}^{2}}{{b}^{2}+{a}^{2}{b}^{2}}$+$\frac{{b}^{2}{m}^{2}-{a}^{2}{b}^{2}{k}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$=$\frac{{(a}^{2}+{b}^{2}){m}^{2}-{a}^{2}{b}^{2}(1+{k}^{2})}{{b}^{2}+{a}^{2}{k}^{2}}$=0,
则(a2+b2)m2=a2b2(1+k2),②
将①代入②,$\frac{{a}^{2}+{b}^{2}}{{a}^{2}{b}^{2}}$=$\frac{1}{{r}^{2}}$,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{r}^{2}}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,点到直线的距离公式及向量数量积的坐标运算,考查计算能力,属于中档题.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案| A. | 不可能事件 | B. | 互斥但不对立事件 | ||
| C. | 对立事件 | D. | 以上答案都不对 |
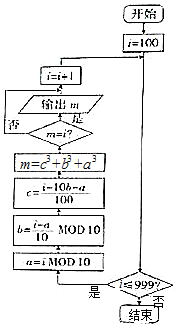 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )①“水仙花数”是三位数;
②152是“水仙花数”;
③407是“水仙花数”.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | y=x2sinx | B. | y=2-x | C. | y=$\frac{sinx}{x}$ | D. | y=|log0.5x| |
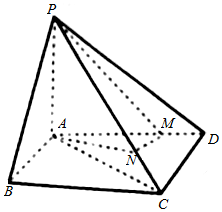 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.