题目内容
 如图,在三棱锥P-ABC中,PA=PB=PC=AC=4,AB=BC=2
如图,在三棱锥P-ABC中,PA=PB=PC=AC=4,AB=BC=2| 2 |
(1)求证:平面ABC⊥平面APC;
(2)求直线PA与平面PBC所成角的正弦值;
(3)若动点M在底面△ABC内(包含边界),二面角M-PA-C的余弦值为
3
| ||
| 10 |
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)证明平面ABC⊥平面APC,利用线面垂直证明,即证OP⊥平面ABC;
(2)作BC的中点E,连结PE,AE,利用面面垂直的判定定理得出平面PBC⊥平面PED,作PC的中点F,又D为AC的中点,推断出AP∥DF,进而可知直线PA与平面PBC所成角与直线DF与平面PBC所成角相等,有D向PE作垂线,交PE与G,判断出∠DFG为直线DF与平面PBC所成角,利用勾股定理求得PE,在Rt△PDE中,利用射影定理求得DG,在Rt△DGF中,求得sin∠DFG,即直线PA与平面PBC所成角的正弦值.
(3)平面PAC的法向量
=
=(2,0,0),求出平面PAM的法向量,利用二面角M-PA-C的余弦值为
,可得n+2=
m,从而可求B点到AM的最小值.
(2)作BC的中点E,连结PE,AE,利用面面垂直的判定定理得出平面PBC⊥平面PED,作PC的中点F,又D为AC的中点,推断出AP∥DF,进而可知直线PA与平面PBC所成角与直线DF与平面PBC所成角相等,有D向PE作垂线,交PE与G,判断出∠DFG为直线DF与平面PBC所成角,利用勾股定理求得PE,在Rt△PDE中,利用射影定理求得DG,在Rt△DGF中,求得sin∠DFG,即直线PA与平面PBC所成角的正弦值.
(3)平面PAC的法向量
| n2 |
| OB |
3
| ||
| 10 |
|
解答:
(1)证明:作AC的中点D,连结PD,BD,
∵PA=PC,
∴PD⊥AC,
∵PA=PB=AC=4,
∴∠PAC=60°,PD=
AD=2
,
∵AB=BC=2
,AC=4,
∴AC2=AB2+B2,
∴∠ABC=90°,∠ACB=45°,
∴BD=CD=2,
∴PB2=PD2+DB2,
∴PD⊥BD,
∵BD?平面ABC,AC?平面ABC,BD∩AC=D,
∴PD⊥平面ABC,
∵PD?平面APC,
∴平面ABC⊥平面APC.
(2)作BC的中点E,连结PE,AE,
∵PB=PC,AB=AC,
∴PE⊥BC,AE⊥BC,
∵PE?平面PDE,AE?平面PDE,PE∩AE=E,
∴BC⊥平面PDE,
∵BC?平面PBC,
∴平面PBC⊥平面PED,
作PC的中点F,又D为AC的中点,
∴AP∥DF,
∴直线PA与平面PBC所成角与直线DF与平面PBC所成角相等,
有D向PE作垂线,交PE与G,
∵平面PBC⊥平面PED,平面PBC∩平面PED=PE,
∴DG⊥平面PBC,连结DF,
则∠DFG为直线DF与平面PBC所成角,
PD=2
,DE=
AB=
,DF=
AP=2
∴PE=
=
,
∴在Rt△PDE中,DG=
=
=
,
在Rt△DGF中,sin∠DFG=
=
×
=
,
即直线PA与平面PBC所成角的正弦值为
.
(3)以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图所示空间直角坐标系.
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2
),
有题意平面PAC的法向量
=
=(2,0,0),
设平面PAM的法向量
=(x,y,z),M=(m,n,0),
∵
=(0,2,2
),
=(m,n+2,0),
•
=0,
•
=0,
∴
,
取y=-1,可得
=(
,-1,
),
∴cos<
,
>=
=
,
∴n+2=
n,
∴BM的最小值为垂直距离d=
.
∵PA=PC,
∴PD⊥AC,
∵PA=PB=AC=4,
∴∠PAC=60°,PD=
| 3 |
| 3 |
∵AB=BC=2
| 2 |
∴AC2=AB2+B2,
∴∠ABC=90°,∠ACB=45°,
∴BD=CD=2,
∴PB2=PD2+DB2,
∴PD⊥BD,
∵BD?平面ABC,AC?平面ABC,BD∩AC=D,
∴PD⊥平面ABC,
∵PD?平面APC,
∴平面ABC⊥平面APC.
(2)作BC的中点E,连结PE,AE,
∵PB=PC,AB=AC,
∴PE⊥BC,AE⊥BC,
∵PE?平面PDE,AE?平面PDE,PE∩AE=E,
∴BC⊥平面PDE,
∵BC?平面PBC,
∴平面PBC⊥平面PED,
作PC的中点F,又D为AC的中点,
∴AP∥DF,
∴直线PA与平面PBC所成角与直线DF与平面PBC所成角相等,
有D向PE作垂线,交PE与G,
∵平面PBC⊥平面PED,平面PBC∩平面PED=PE,
∴DG⊥平面PBC,连结DF,
则∠DFG为直线DF与平面PBC所成角,
PD=2
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
∴PE=
| PD2+DE2 |
| 14 |
∴在Rt△PDE中,DG=
| PD•DE |
| PE |
2
| ||||
|
2
| ||
|
在Rt△DGF中,sin∠DFG=
| DG |
| DF |
2
| ||
|
| 1 |
| 2 |
| ||
| 7 |
即直线PA与平面PBC所成角的正弦值为
| ||
| 7 |
(3)以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图所示空间直角坐标系.
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2
| 3 |
有题意平面PAC的法向量
| n2 |
| OB |
设平面PAM的法向量
| n3 |
∵
| AP |
| 3 |
| AM |
| AP |
| n3 |
| AM |
| n3 |
∴
|
取y=-1,可得
| n3 |
| n+2 |
| m |
| ||
| 3 |
∴cos<
| n2 |
| n3 |
| ||||||
2
|
2
| ||
| 3 |
∴n+2=
|
∴BM的最小值为垂直距离d=
8
| ||||
| 35 |
点评:本题考查面面垂直,考查线面角,考查平面法向量的求解,解题的关键是掌握面面垂直的判定,正确求出平面的法向量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知cosθ-sinθ=
,则sin2θ=( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
复数z=
,|
|是( )
| 5 |
| 3+4i |
. |
| z |
| A、25 | B、5 | C、1 | D、7 |
函数f(x)=lnx+
的零点所在的区间是( )
| 1 |
| 2 |
| A、(e-4,e-2) |
| B、(e-2,1) |
| C、(1,e2) |
| D、(e2,e4) |
等差数列{an}中,a1+a5=6,a6=5,那么a9的值是( )
| A、-7 | ||
| B、7 | ||
C、-
| ||
D、
|
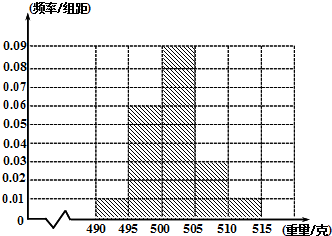 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.