题目内容
(1)求证:对任意的正实数x,不等式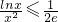 都成立.
都成立.
(2)求证:对任意的n∈N*,不等式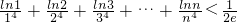 总成立.
总成立.
(1)证明:设函数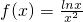 ,则
,则 .令f'(x)=0,得x=
.令f'(x)=0,得x= .
.
当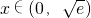 时,f'(x)>0,故函数f(x)在
时,f'(x)>0,故函数f(x)在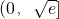 上递增;
上递增;
当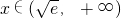 时,f'(x)<0,故函数f(x)在
时,f'(x)<0,故函数f(x)在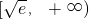 上递减;
上递减;
所以 ,对任意的x>0,不等式
,对任意的x>0,不等式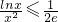 总成立.
总成立.
(2)证明:由(1)知:对x∈(0,+∞)均有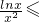
 ,故
,故 .
.
当n=1时,结论显然成立;
当n≥2时,有: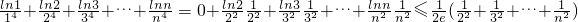
 .
.
综上可知,对任意的n∈N*,不等式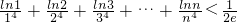 成立.
成立.
分析:(1)构造函数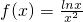 ,求导函数,确定函数的单调性与极值,即可证得结论;
,求导函数,确定函数的单调性与极值,即可证得结论;
(2)由(1)知:对x∈(0,+∞)均有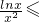
 ,故
,故 ,由此利用放缩法及裂项法,即可证得结论.
,由此利用放缩法及裂项法,即可证得结论.
点评:本题考查不等式的证明,考查构造函数,利用导函数研究函数的单调性与极值,解题的关键是构造函数、确定函数的单调性.
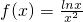 ,则
,则 .令f'(x)=0,得x=
.令f'(x)=0,得x= .
.当
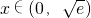 时,f'(x)>0,故函数f(x)在
时,f'(x)>0,故函数f(x)在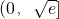 上递增;
上递增;当
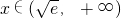 时,f'(x)<0,故函数f(x)在
时,f'(x)<0,故函数f(x)在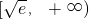 上递减;
上递减;所以
 ,对任意的x>0,不等式
,对任意的x>0,不等式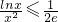 总成立.
总成立.(2)证明:由(1)知:对x∈(0,+∞)均有
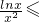
 ,故
,故 .
.当n=1时,结论显然成立;
当n≥2时,有:
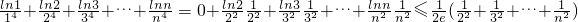
 .
.综上可知,对任意的n∈N*,不等式
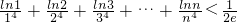 成立.
成立.分析:(1)构造函数
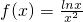 ,求导函数,确定函数的单调性与极值,即可证得结论;
,求导函数,确定函数的单调性与极值,即可证得结论;(2)由(1)知:对x∈(0,+∞)均有
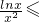
 ,故
,故 ,由此利用放缩法及裂项法,即可证得结论.
,由此利用放缩法及裂项法,即可证得结论.点评:本题考查不等式的证明,考查构造函数,利用导函数研究函数的单调性与极值,解题的关键是构造函数、确定函数的单调性.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
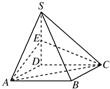 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).