题目内容
已知直线 经过点
经过点 ,且和圆
,且和圆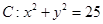 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线 的方程。
的方程。

解析试题分析:当 的斜率不存在时,方程为
的斜率不存在时,方程为 =5,
=5,
与圆C相切,不满足题目要求
设直线 的斜率为
的斜率为 ,则
,则 的方程
的方程 .
.
如图所示, 设
设 是圆心到直线
是圆心到直线 的距离,
的距离, 是圆的半径,则
是圆的半径,则 是弦长
是弦长 的一半,
的一半,
在 中,
中, =5.
=5.  =
=
 =
= ×4
×4 =2
=2 .
.
所以  ,
,
所以满足条件的直线方程为
又知  ,解得
,解得 =
= 或
或 =
= .
.
考点:直线的一般式方程;直线与圆相交的性质.
点评:考查学生掌握直径与圆的弦垂直时直径平分这条弦的运用,会利用点到直线的距离公式化简求值.此
题是一道综合题,要求学生掌握的知识要全面,解k时注意两种情况都满足.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 中,点
中,点 ,直线
,直线 。设圆
。设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围。
的取值范围。 中,点
中,点 ,直线
,直线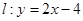 ,设圆
,设圆 的半径为1, 圆心在
的半径为1, 圆心在 上.
上.
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围. ,
, 交于A、B两点;
交于A、B两点; 上的圆的方程.
上的圆的方程. 是圆
是圆 上的动点,
上的动点, 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点. ,直线
,直线 :
: .
. 时,求直线
时,求直线 直线
直线 .
. 相切, 且与直线
相切, 且与直线 平行的直线
平行的直线 的方程;
的方程; 与圆
与圆 轴上的截距
轴上的截距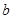 的取值范围.
的取值范围. 作圆C:
作圆C: 的切线,切点为D,且QD=4.
的切线,切点为D,且QD=4. 的值;
的值; ,求
,求 的最小值(O为坐标原点).
的最小值(O为坐标原点).