题目内容
(12分)过点Q  作圆C:
作圆C: 的切线,切点为D,且QD=4.
的切线,切点为D,且QD=4.
(1)求 的值;
的值;
(2)设P是圆C上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y 轴于点B,设 ,求
,求 的最小值(O为坐标原点).
的最小值(O为坐标原点).
(1)  (2)
(2) 取得最小值为6。
取得最小值为6。
解析试题分析:(1)由题设知, 是以D为直角顶点的直角三角形,结合勾股定理得到r的值。
是以D为直角顶点的直角三角形,结合勾股定理得到r的值。
(2)根据线与圆相切以及均值不等式和向量的坐标关系得到。
解:(1) 圆C: 的圆心为O(0,0),于是
的圆心为O(0,0),于是
由题设知, 是以D为直角顶点的直角三角形,
是以D为直角顶点的直角三角形,
故有
(2)设直线 的方程为
的方程为 即
即 
则


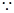 直线
直线 与圆C相切
与圆C相切


当且仅当 时取到“=”号
时取到“=”号 取得最小值为6。
取得最小值为6。
考点:本试题主要考查了直线与圆的位置关系的运用。
点评:解决该试题的关键是利用线圆相切则有圆心到直线的距离于圆的半径。

练习册系列答案
相关题目
 经过点
经过点 ,且和圆
,且和圆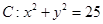 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线
 ,求直线l的方程.
,求直线l的方程. :
: ,设点
,设点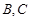 是直线
是直线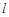 :
: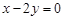 上的两点,它们的横坐标分别
上的两点,它们的横坐标分别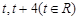 ,
,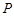 点的纵坐标为
点的纵坐标为 且点
且点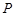 在线段
在线段 上,过
上,过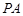 ,切点为
,切点为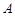
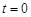 ,
,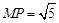 ,求直线
,求直线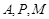 三点的圆的圆心是
三点的圆的圆心是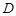 ,
,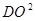 表示成
表示成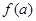 ,并写出定义域.
,并写出定义域.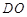 长的最小值
长的最小值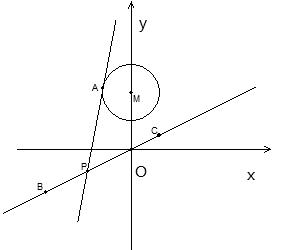
 和直线
和直线
 取什么值,直线和圆总相交;
取什么值,直线和圆总相交; ,圆
,圆
 和圆
和圆 的位置关系;
的位置关系; 的值.
的值. 经过
经过 、
、 两点,且圆心在直线
两点,且圆心在直线 上.
上.  经过点
经过点