题目内容
(本小题满分14分)
已知,圆C: ,直线
,直线 :
: .
.
(1) 当a为何值时,直线 与圆C相切;
与圆C相切;
(2) 当直线 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且 时,求直线
时,求直线 的方程.
的方程.
(1)  . (2)直线
. (2)直线 的方程是
的方程是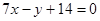 和
和 .
.
解析试题分析:将圆C的方程 配方得标准方程为
配方得标准方程为 ,则此圆的圆心为(0 , 4),半径为2. ……………………………2分
,则此圆的圆心为(0 , 4),半径为2. ……………………………2分
(1) 若直线 与圆C相切,则有
与圆C相切,则有 . ………………4分
. ………………4分
解得 . 6分
. 6分
(2) 解法一:过圆心C作CD⊥AB, 7分
则根据题意和圆的性质,得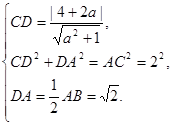 10分
10分
解得 . 12分
. 12分
(解法二:联立方程 并消去
并消去 ,得
,得 .
.
设此方程的两根分别为 、
、 ,则用
,则用 即可求出a.)
即可求出a.)
∴直线 的方程是
的方程是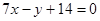 和
和 . 14分
. 14分
考点:本题考查了直线与圆的位置关系
点评:研究直线和圆的位置关系的相关问题时通常采用“几何法”即抓住圆心到直线的的距离与半径的关系

练习册系列答案
相关题目
 中,点A(0,3),直线
中,点A(0,3),直线 :
: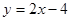 ,设圆
,设圆 的半径为1,圆心在
的半径为1,圆心在
 上,过点A作圆
上,过点A作圆 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围. 与圆C相切.
与圆C相切. 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B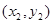 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积. 经过点
经过点 ,且和圆
,且和圆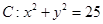 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点。
交圆C于A、B两点。 时,写出直线
时,写出直线 ,圆
,圆 .
.
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 同时平分圆
同时平分圆 .
. )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
 ,圆
,圆
 和圆
和圆 的位置关系;
的位置关系; 的值.
的值.