题目内容
已知圆 ,
, 交于A、B两点;
交于A、B两点;
(1)求过A、B两点的直线方程;
(2)求过A、B两点,且圆心在直线 上的圆的方程.
上的圆的方程.
(1)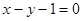 (2)
(2)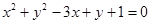
解析试题分析:(1)过圆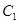 与圆
与圆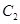 交点的直线,即为两圆公共弦的直线.
交点的直线,即为两圆公共弦的直线.
所以过A、B两点的直线方程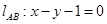 . 5分
. 5分
(2)设所求圆的方程为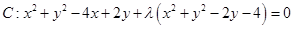 . 6分
. 6分
则圆心坐标为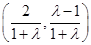 8分
8分
∵圆心在直线 上
上
∴将圆心坐标代入直线方程,得 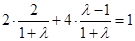 9分
9分
解得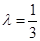 . 11分
. 11分
∴所求圆的方程为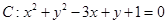 . 12分
. 12分
考点:圆与圆的位置关系与圆的方程
点评:两圆相交时,其公共弦所在直线方程只需将两圆方程相减即可,求解圆的方程的题目常采用待定系数法:设出圆的方程,根据条件列出关于参数的方程组,解方程组得到参数值最后写出方程

练习册系列答案
相关题目
 ,求l的方程;
,求l的方程; 与直线l:
与直线l: ,且直线l被圆C截得的弦长为
,且直线l被圆C截得的弦长为 .
.  的值;
的值;  时,求过点(3,5)且与圆C相切的直线方程.
时,求过点(3,5)且与圆C相切的直线方程.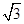 ,半径小于5.
,半径小于5. 与圆C相切.
与圆C相切. 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B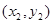 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积. 和圆
和圆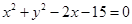 相交于点
相交于点 。
。 的垂直平分线方程;(2)求弦
的垂直平分线方程;(2)求弦 经过点
经过点 ,且和圆
,且和圆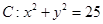 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线 ,圆
,圆 .
.
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 同时平分圆
同时平分圆 ,求直线l的方程.
,求直线l的方程.