题目内容

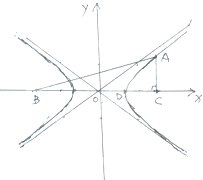如图，直角坐标系xoy中，有Rt△ABC，∠C=90°，D在边BC上，BD=3DC，双曲线E以B、C为焦点，且经过A、D两点．
（1）求双曲线E的渐近线方程；
（2）若△ABC的周长为12，求双曲线的方程．
分析：（1）设双曲线E的方程为
x2
a2
-
y2
b2
=1（a＞0，b＞0），由B（-c，0），D（a，0），C（c，0）．BD=3DC，得c+a=3（c-a），由此能求出双曲线E的渐近线方程；
（2）由（1）即可得到双曲线E的方程．
解答：解：设双曲线E的方程为
x2
a2
-
y2
b2
=1（a＞0，b＞0），
则B（-c，0），D（a，0），C（c，0）．
由BD=3DC，得c+a=3（c-a），即c=2a．
∴
|AB|2-|AC|2=16a2
|AB|+|AC|=12-4a
|AB|-|AC|=2a
…（3分）
解之得a=1，∴c=2，b=
3
．
∴（1）双曲线E的渐近线方程y=±
3
x；
（2）双曲线E的方程为x2-
y2
3
=1．…（5分）
点评：本题考查双曲线方程的求法，解题时要认真审题，注意等价转化思想的合理运用．
练习册系列答案
相关题目
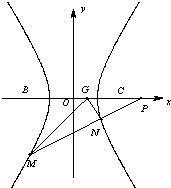如图，直角坐标系xOy中，一直角三角形ABC，∠C=90°，B、C在x轴上且关于原点O对称，D在边BC上，BD=3DC，△ABC的周长为12．若一双曲线E以B、C为焦点，且经过A、D两点．
（1）求双曲线E的方程；
（2）若一过点P（m，0）（m为非零常数）的直线l与双曲线E相交于不同于双曲线顶点的两点M、N，且
MP
=λ
PN
，问在x轴上是否存在定点G，使
BC
⊥(
GM
-λ
GN
)？若存在，求出所有这样定点G的坐标；若不存在，请说明理由．
（2012•芜湖二模）如图，直角坐标系XOY中，点F在x轴正半轴上，△OFG的面积为S．且
OF
•
FG
=1，设|
OF
|=c(c≥2)，S=
3
4
c．
（1）以O为中心，F为焦点的椭圆E经过点G，求点G的纵坐标．
（2）在（1）的条件下，当|
OG
|取最小值时，求椭圆E的标准方程．
（3）在（2）的条件下，设点A、B分别为椭圆E的左、右顶点，点C是椭圆的下顶点，点P在椭圆E上（与点A、B均不重合），点D在直线PA上，若直线PB的方程为，且
AP
•
CD
=0，试求CD直线方程．
（2012•蓝山县模拟）如图，直角坐标系xOy中，一直角三角形ABC，∠=90°，B、C在x轴上且关于原点O对称，D在边BC上，BD=3DC，△ABC的周长为12．若一双曲线E以B、C为焦点，且经过A、D两点．
（1）求双曲线E的方程；
（ 2）若一过点O（m，0）（m为非零常数）的直线与双曲线E相交于不同于双曲线顶点的两点M、N，且
MP
=λ
PN
，问在x轴上是否存在定点G，使
BC
⊥(
GM
-λ
GN
)？若存在，求出所有这样定点G的坐标；若不存在，请说明理由．
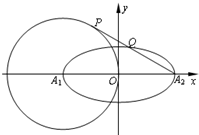精英家教网如图平面直角坐标系xOy中，椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率e=
3
2
，A1，A2分别是椭圆的左、右两个顶点，圆A1的半径为a，过点A2作圆A1的切线，切点为P，在x轴的上方交椭圆于点Q．则
PQ
QA2
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网