Question

（2012•蓝山县模拟）如图，直角坐标系xOy中，一直角三角形ABC，∠=90°，B、C在x轴上且关于原点O对称，D在边BC上，BD=3DC，△ABC的周长为12．若一双曲线E以B、C为焦点，且经过A、D两点．
（1）求双曲线E的方程；
（ 2）若一过点O（m，0）（m为非零常数）的直线与双曲线E相交于不同于双曲线顶点的两点M、N，且

MP

=λ

PN

，问在x轴上是否存在定点G，使

BC

⊥(

GM

-λ

GN

)？若存在，求出所有这样定点G的坐标；若不存在，请说明理由．

Answer 1

分析：（1）设双曲线E的方程为

x2

a2

-

y2

b2

=1  (a＞0，b＞0)，由B（-c，0），D（a，0），C（c，0）．BD=3DC，得c+a=3（c-a），由此能求出双曲线E的方程．
（2）设在x轴上存在定点G（t，0），使

BC

⊥(

GM

-λ

GN

)．设直线l的方程为x-m=ky，M（x₁，y₁），N（x₂，y₂）．由

MP

=λ

PN

，得y₁+λy₂=0．由此能推导出在x轴上存在定点G(

1

m

，0)，使

BC

⊥(

GM

-λ

GN

)．

解答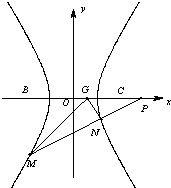：（本小题满分13分）
解：（1）设双曲线E的方程为

x2

a2

-

y2

b2

=1  (a＞0，b＞0)，
则B（-c，0），D（a，0），C（c，0）．
由BD=3DC，得c+a=3（c-a），即c=2a．
∴

|AB|2-|AC|2=16a2 |AB|+|AC|=12-4a |AB|-|AC|=2a.

…（3分）
解之得a=1，∴c=2，  b=

3

．
∴双曲线E的方程为x2-

y2

3

=1．…（5分）
（2）设在x轴上存在定点G（t，0），使

BC

⊥(

GM

-λ

GN

)．
设直线l的方程为x-m=ky，M（x₁，y₁），N（x₂，y₂）．
由

MP

=λ

PN

，得y₁+λy₂=0．
即λ=-

y1

y2

①…（6分）
∵

BC

=(4，0)，

GM

-λ

GN

=(x1-t-λx2+λt， y1-λy2)，
∴

BC

⊥(

GM

-λ

GN

)?x₁-t=λ（x₂-t）．
即ky₁+m-t=λ（ky₂+m-t）．②…（8分）
把①代入②，得2ky₁y₂+（m-t）（y₁+y₂）=0③…（10分）
把x-m=ky代入x2-

y2

3

=1，并整理得（3k²-1）y²+6kmy+3（m²-1）=0，
其中3k²-1≠0且△＞0，即k2≠

1

3

且3k²+m²＞1．
y1+y2=

-6km

3k2-1

，  y1y2=

3(m2-1)

3k2-1

．…（11分）
代入③，得

6k(m2-1)

3k2-1

-

6km(m-t)

3k2-1

=0，
化简得 kmt=k．
当t=

1

m

时，上式恒成立．
因此，在x轴上存在定点G(

1

m

，0)，使

BC

⊥(

GM

-λ

GN

)．…（13分）

点评：本题考查双曲线方程的求法，考查定点坐标是否存在的探索，解题时要认真审题，注意等价转化思想的合理运用．