题目内容
13. 某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了200件产品的净重,所得数据均在区间[96,106]上,其频率分布直方图如图所示,已知各个小方形按高度依次构成一个等差数列,则在抽测的200件产品中,净重在区间[98,102)上的产品件数是100.
某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了200件产品的净重,所得数据均在区间[96,106]上,其频率分布直方图如图所示,已知各个小方形按高度依次构成一个等差数列,则在抽测的200件产品中,净重在区间[98,102)上的产品件数是100.
分析 设出各个小方形按高度依次构成的等差数列公差为x,根据频率和列出方程求出x的值,再计算在区间[98,102)上的频率与频数即可.
解答 解:根据题意,设各个小方形按高度依次构成的等差数列公差为x,
则0.050+a+b+c+d=5×0.050+$\frac{1}{2}$×5×4x=0.5,
解得x=0.025,
所以a=0.075,b=0.10,c=0.125,d=0.15;
所以该批产品中净重在区间[98,102)上的频率为:
2(b+d)=2×(0.10+0.15)=0.5,
故所求的产品件数是100×0.5=100.
故答案为:100.
点评 本题考查了频率分布直方图的应用问题,也考查了等差数列的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.运行如图所示的程序框图后,输出的m值是( )
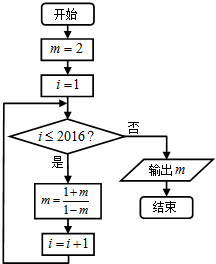

| A. | -3 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
4.已知a=log25,b=log5(log25),c=($\frac{1}{2}$)-0.52,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | b<a<c |
1.在复平面内复数$z=\frac{{|2\sqrt{3}-2i|+bi}}{1-i}({b>0})$的模为$\sqrt{26}$,则复数z-bi在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知向量$\overrightarrow a=(1,2)$,$\overrightarrow b=(3,x)$,$\overrightarrow c=(x,4)$,若$(\overrightarrow a-\overrightarrow b)∥\overrightarrow c$,则x=( )
| A. | 2或-4 | B. | -2或4 | C. | $\frac{2}{3}$ | D. | $-\frac{2}{3}$ |
 广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图的频率分布直方图.问:
广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图的频率分布直方图.问: