题目内容
已知函数f(x)是(-∞,+∞)上的增函数,a、b∈R,对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”.
(1)写出其逆命题,判断其真假,并证明你的结论;
(2)写出其逆否命题,判断其真假,并证明你的结论.
解 (1)逆命题是:若f(a)+f(b)≥f(-a)+f(-b),
则a+b≥0为真命题.
用反证法证明:假设a+b<0,则a<-b,b<-a.
∵f(x)是(-∞,+∞)上的增函数,
则f(a)<f(-b),f(b)<f(-a),
∴f(a)+f(b)<f(-a)+f(-b),这与题设相矛盾,所以逆命题为真.
(2)逆否命题:若f(a)+f(b)<f(-a)+f(-b),
则a+b<0为真命题.
因为原命题⇔它的逆否命题,所以证明原命题为真命题即可.
∵a+b≥0, ∴a≥-b,b≥-a.
又∵f(x)在(-∞,+∞)上是增函数,
∴f(a)≥f(-b),f(b)≥f(-a),
∴f(a)+f(b)≥f(-a)+f(-b).
所以逆否命题为真.

练习册系列答案
相关题目
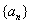 中,若
中,若 ,
, ,则
,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.
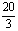 ,椭圆C2的方程为
,椭圆C2的方程为 ,C2的离心率为
,C2的离心率为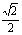 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求: a∈(0,+∞),
a∈(0,+∞), θ∈R,使asinθ≥a成立,则cos(θ-
θ∈R,使asinθ≥a成立,则cos(θ- )的值为 .
)的值为 . 则f(f(-2))=________.
则f(f(-2))=________.