题目内容
18.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点F作一条渐近线的垂线,垂足为点A,与另一条渐进线交于点B,若$\overrightarrow{FB}$=2$\overrightarrow{FA}$,则此双曲线的离心率为2.分析 方法一:求得渐近线方程,联立求得A,B坐标,根据向量数量积坐标运算,整理即可求得双曲线的离心率;
方法二:先由$\overrightarrow{FB}$=2$\overrightarrow{FA}$得出A为线段FB的中点,再借助于图象分析出其中一条渐近线对应的倾斜角的度数,找到a,b之间的等量关系,进而求出双曲线的离心率.
解答 解:方法一:由题意得左焦点F(-c,0),
设一渐近线OA的方程为y=-$\frac{b}{a}$x,另一渐近线OB的方程为y=$\frac{b}{a}$x,
由FA的方程为y=$\frac{a}{b}$(x+c),则$\left\{\begin{array}{l}{y=\frac{a}{b}(x+c)}\\{y=-\frac{b}{a}x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-\frac{{a}^{2}}{c}}\\{y=\frac{ab}{c}}\end{array}\right.$,
则A(-$\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
$\left\{\begin{array}{l}{y=\frac{a}{b}(x+c)}\\{y=\frac{b}{a}x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{{a}^{2}c}{{b}^{2}-{a}^{2}}}\\{y=\frac{abc}{{b}^{2}-{a}^{2}}}\end{array}\right.$,
则B($\frac{{a}^{2}c}{{b}^{2}-{a}^{2}}$,$\frac{abc}{{b}^{2}-{a}^{2}}$)
由$\overrightarrow{FB}$=2$\overrightarrow{FA}$,可得2(-$\frac{{a}^{2}}{c}$+c)=$\frac{{a}^{2}c}{{b}^{2}-{a}^{2}}$+c,
即为-$\frac{2{a}^{2}}{c}$+2c=$\frac{{a}^{2}c}{{c}^{2}-2{a}^{2}}$+c,整理得:c4-5a2c2+4a4=0,
由e=$\frac{c}{a}$,等式两边同除以a4,整理得:c4-5e2+4=0,
解得e2=4或e2=1,
由e>1,
∴e=2.
故答案为:2.
方法二:如图$\overrightarrow{FB}$=2$\overrightarrow{FA}$,则A为线段FB的中点,
∴∠2=∠4,又∠1=∠3,∠2+∠3=90°,所以∠1=∠2+∠4=2∠2=∠3.
故∠2+∠3=90°=3∠2,∠2=30°⇒∠1=60°,$\frac{b}{a}$=$\sqrt{3}$.
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+(\sqrt{3})^{2}}$=2,则e=2.
故答案为:2.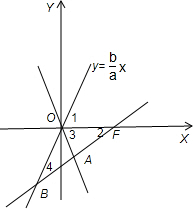
点评 本题考查双曲线的标准方程及简单几何性质,考查双曲线的离心率公式,考查计算能力,属于中档题.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案参考数据
P(μ-σ<X≤μ+σ)=0.6826
P(μ-2σ<X≤μ+2σ)=0.9544
P(μ-3σ<X≤μ+3σ)=0.9974.
| A. | 0.6826 | B. | 0.9544 | C. | 0.2718 | D. | 0.1359 |
| A. | 18个 | B. | 16个 | C. | 14个 | D. | 12个 |
| A. | 3种 | B. | 4种 | C. | 6种 | D. | 8种 |
| A. | y=-2 | B. | y=2 | C. | x=-2 | D. | x=2 |
 近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下表示.
近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下表示. | 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 0.100 | |
| 第2组 | [165,170) | ① | |
| 第3组 | [170,175) | 20 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
(2)为了能选拔出最优秀的选手,组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名学生进入第二轮面试,求第3、4、5组每组各抽取多少名选手进入第二轮面试;
(3)在(2)的前提下,组委会决定在5名选手中随机抽取2名选手接受A考官进行面试,求:第4组至少有一名选手被考官A面试的概率.
| A. | $\sqrt{7}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | $\sqrt{13}$ |