题目内容
已知焦点在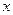 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为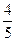 ,且过点
,且过点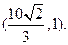
(1)求椭圆C的方程;
(2)直线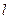 分别切椭圆C与圆
分别切椭圆C与圆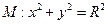 (其中
(其中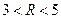 )于A.B两点,求|AB|的最大值。
)于A.B两点,求|AB|的最大值。
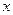 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为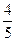 ,且过点
,且过点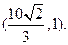
(1)求椭圆C的方程;
(2)直线
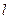 分别切椭圆C与圆
分别切椭圆C与圆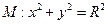 (其中
(其中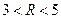 )于A.B两点,求|AB|的最大值。
)于A.B两点,求|AB|的最大值。(1)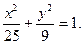
(2)2
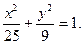
(2)2
(1)设椭圆的方程为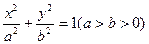 ,则
,则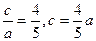 ,
,
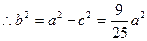
 椭圆过点
椭圆过点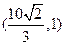
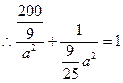 ,
,
解处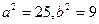 故椭圆C的方程为
故椭圆C的方程为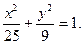 6分
6分
(2)设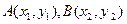 分别为直线
分别为直线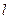 与椭圆和圆的切点,
与椭圆和圆的切点,
直线AB的方程为: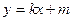 因为A既在椭圆上,又在直线AB上,
因为A既在椭圆上,又在直线AB上,
从而有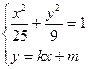 ,
,
消去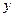 得:
得: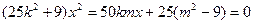
由于直线与椭圆相切,
故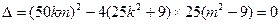
从而可得: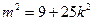 ①
① 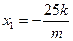 ②……8分
②……8分
由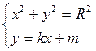 消去
消去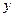 得:
得:
由于直线与圆相切,得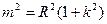 ③
③ 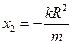
 ④
④
由②④得: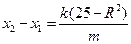 由①③得:
由①③得: ……10分
……10分
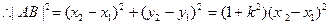
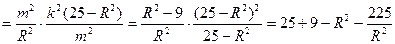
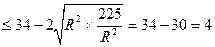
即
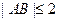 ,当且仅当
,当且仅当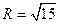 时取等号,所以|AB|的最大值为2。……12分
时取等号,所以|AB|的最大值为2。……12分
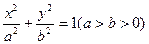 ,则
,则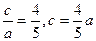 ,
,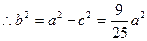
 椭圆过点
椭圆过点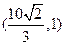
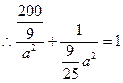 ,
,解处
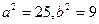 故椭圆C的方程为
故椭圆C的方程为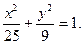 6分
6分(2)设
 分别为直线
分别为直线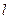 与椭圆和圆的切点,
与椭圆和圆的切点,直线AB的方程为:
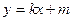 因为A既在椭圆上,又在直线AB上,
因为A既在椭圆上,又在直线AB上,从而有
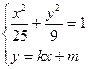 ,
,消去
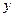 得:
得: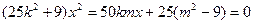
由于直线与椭圆相切,
故
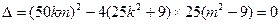
从而可得:
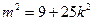 ①
① 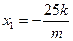 ②……8分
②……8分由
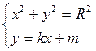 消去
消去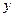 得:
得:
由于直线与圆相切,得
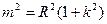 ③
③ 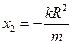
 ④
④由②④得:
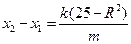 由①③得:
由①③得: ……10分
……10分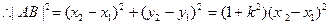
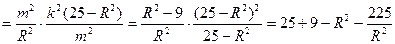
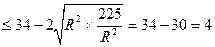
即

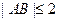 ,当且仅当
,当且仅当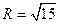 时取等号,所以|AB|的最大值为2。……12分
时取等号,所以|AB|的最大值为2。……12分
练习册系列答案
相关题目
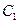 :
: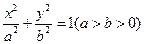 ,抛物线
,抛物线 :
: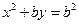 .
.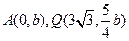 ,又
,又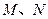 为
为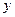 轴上的两个交点,若
轴上的两个交点,若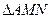 的垂心为
的垂心为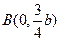 ,且
,且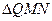 的重心在
的重心在 的方程.
的方程.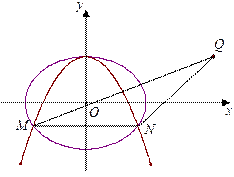
 轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
轴上,椭圆C上的点到焦点的最大值为3,最小值为1. :
: 与
与 椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线
椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线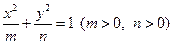 与曲线
与曲线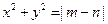 无交点,则椭圆的离心率
无交点,则椭圆的离心率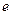 的取值范围是
的取值范围是
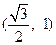
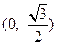
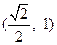

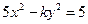 的一个焦点为(0,2),则
的一个焦点为(0,2),则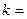 ( )
( )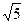
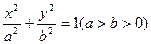 ,
,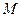 、
、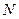 是椭圆上关于原点对称的两点,
是椭圆上关于原点对称的两点,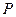 是椭圆上任意一点,且直线
是椭圆上任意一点,且直线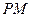 、
、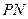 的斜率分别为
的斜率分别为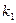 、
、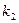 ,若
,若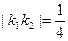 ,则椭圆的离心率为( )
,则椭圆的离心率为( )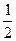

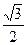
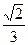
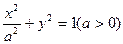 的一条准线经过抛物线
的一条准线经过抛物线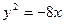 的焦点,则该椭圆的离心率为 ( )
的焦点,则该椭圆的离心率为 ( )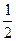
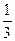

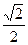
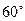 的菱形的四个顶点,则椭圆的离心率为 .
的菱形的四个顶点,则椭圆的离心率为 .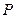 为椭圆上任一点(不是长轴顶点),过点
为椭圆上任一点(不是长轴顶点),过点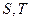 ,求证以线段
,求证以线段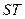 为直径的圆过这个椭圆的两个焦点
为直径的圆过这个椭圆的两个焦点