题目内容
(本小题满分12分)
设椭圆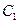 :
: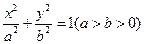 ,抛物线
,抛物线 :
: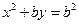 .
.
(1) 若 经过
经过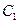 的两个焦点,求
的两个焦点,求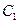 的离心率;
的离心率;
(2) 设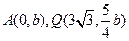 ,又
,又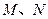 为
为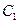 与
与 不在
不在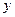 轴上的两个交点,若
轴上的两个交点,若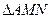 的垂心为
的垂心为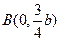 ,且
,且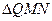 的重心在
的重心在 上,求椭圆
上,求椭圆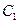 和抛物线
和抛物线
 的方程.
的方程.
设椭圆
 :
: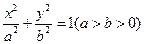 ,抛物线
,抛物线 :
: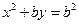 .
.(1) 若
 经过
经过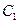 的两个焦点,求
的两个焦点,求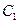 的离心率;
的离心率;(2) 设
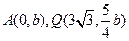 ,又
,又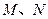 为
为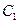 与
与 不在
不在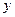 轴上的两个交点,若
轴上的两个交点,若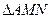 的垂心为
的垂心为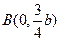 ,且
,且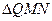 的重心在
的重心在 上,求椭圆
上,求椭圆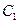 和抛物线
和抛物线
 的方程.
的方程.
(1)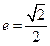 (2)椭圆
(2)椭圆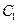 的方程为:
的方程为: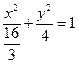 ,抛物线
,抛物线 的方程为:
的方程为: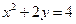 .
.
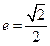 (2)椭圆
(2)椭圆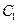 的方程为:
的方程为: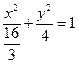 ,抛物线
,抛物线 的方程为:
的方程为: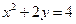 .
.(1)因为抛物线 经过椭圆
经过椭圆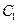 的两个焦点
的两个焦点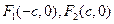 ,可得:
,可得: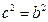 ,
,
由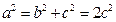 得椭圆
得椭圆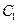 的离心率
的离心率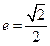 .
.
(2)由题设可知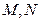 关于
关于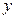 轴对称,设
轴对称,设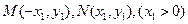 ,
,
则由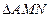 的垂心为
的垂心为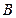 ,有
,有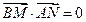 ,
,
所以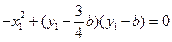
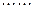 ①
①
由于点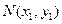 在
在 上,故有
上,故有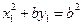
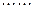 ②
②
②式代入①式并化简得: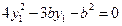 ,解得
,解得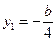 或
或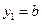 (舍去),
(舍去),
所以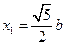 ,故
,故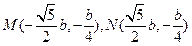 ,
,
所以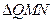 的重心为
的重心为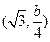 ,
,
因为重心在 上得:
上得: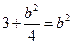 ,所以
,所以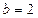 ,
,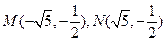 ,
,
又因为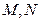 在
在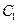 上,所以
上,所以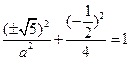 ,得
,得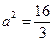 .
.
所以椭圆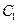 的方程为:
的方程为: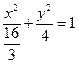 ,
,
抛物线 的方程为:
的方程为: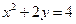 .
.
 经过椭圆
经过椭圆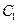 的两个焦点
的两个焦点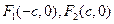 ,可得:
,可得: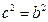 ,
,
由
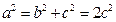 得椭圆
得椭圆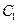 的离心率
的离心率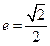 .
.(2)由题设可知
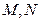 关于
关于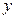 轴对称,设
轴对称,设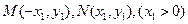 ,
,则由
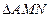 的垂心为
的垂心为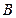 ,有
,有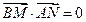 ,
,所以
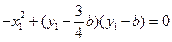
 ①
①由于点
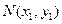 在
在 上,故有
上,故有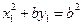
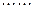 ②
②②式代入①式并化简得:
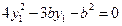 ,解得
,解得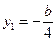 或
或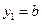 (舍去),
(舍去),所以
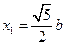 ,故
,故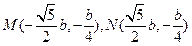 ,
,所以
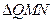 的重心为
的重心为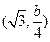 ,
,因为重心在
 上得:
上得: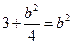 ,所以
,所以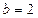 ,
,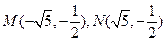 ,
,又因为
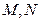 在
在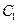 上,所以
上,所以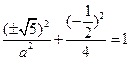 ,得
,得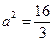 .
.所以椭圆
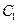 的方程为:
的方程为: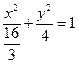 ,
,抛物线
 的方程为:
的方程为: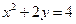 .
.
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
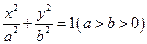 短轴的一个端点
短轴的一个端点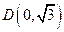 ,离心率
,离心率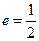 .过
.过 作直线
作直线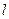 与椭圆交于另一点
与椭圆交于另一点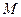 ,与
,与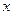 轴交于点
轴交于点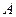 (不同于原点
(不同于原点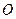 ),点
),点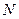 ,直线
,直线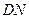 交
交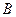 .
.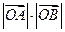 的值.
的值.
 中,椭圆
中,椭圆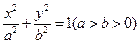 的焦距为2c,以O为圆心,
的焦距为2c,以O为圆心,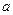 为半径作圆
为半径作圆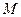 ,若过
,若过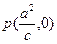 作圆
作圆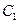 :
: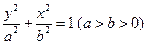 的右顶点为
的右顶点为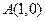 ,过
,过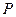 在抛物线
在抛物线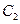 :
: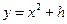
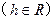 上,
上,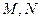 .线段
.线段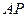 的中点与
的中点与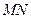 的中点的横坐标相等时,求
的中点的横坐标相等时,求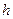 的最小值.
的最小值.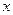 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为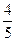 ,且过点
,且过点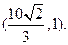
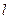 分别切椭圆C与圆
分别切椭圆C与圆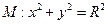 (其中
(其中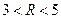 )于A.B两点,求|AB|的最大值。
)于A.B两点,求|AB|的最大值。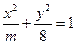 中,F1,F2分别为椭圆的左、右焦点,B、D分别
中,F1,F2分别为椭圆的左、右焦点,B、D分别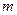 的值;
的值;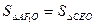 时,求直线AC的方程.
时,求直线AC的方程.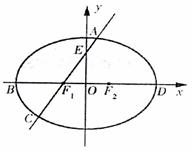
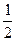
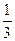
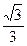
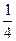
 ,
,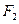 分别为椭圆
分别为椭圆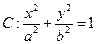
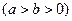 的左右焦点,过
的左右焦点,过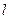 与椭圆
与椭圆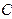 相交于
相交于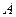 ,
,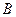 两点,直线
两点,直线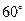 ,
,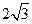 。
。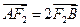 ,求椭圆
,求椭圆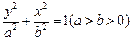 的上焦点为
的上焦点为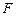 ,左、右顶点分别为
,左、右顶点分别为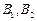 ,下顶点为
,下顶点为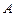 ,直线
,直线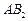 与直线
与直线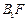 交于点
交于点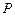 ,若
,若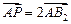 ,则椭圆的离心率为___________。
,则椭圆的离心率为___________。