题目内容
某旅游推介活动晚会进行嘉宾现场抽奖活动,抽奖规则是:抽奖盒中装有 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
(I)活动开始后,一位参加者问:盒中有几个“多彩十艺节”球?主持人笑说:我只知道从盒中同时抽两球不都是“美丽泉城行”标志的概率是 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(Ⅱ)上面条件下,现有甲、乙、丙、丁四人依次抽奖,抽后放回,另一个人再抽,用 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 .
.
【答案】
(I) ;(Ⅱ)分布列如下解析;
;(Ⅱ)分布列如下解析; .
.
【解析】
试题分析:(I)本题获奖的标准是抽到两个球都印有“多彩十艺节”标志即可获奖.而所给的条件是两球不都是“美丽泉城行”标志的概率是 ,不都是是都是的对立面.所以假设有n个标有“美丽泉城行”则都是“美丽泉城行”的概率为
,不都是是都是的对立面.所以假设有n个标有“美丽泉城行”则都是“美丽泉城行”的概率为 .计算出n的值.10-n就是印有“多彩十艺节”球的个数.即可求出抽奖者获奖的概率.(Ⅱ)本小题是一个超几何概型独立性实验.分布列和数学期望及方差公式.
.计算出n的值.10-n就是印有“多彩十艺节”球的个数.即可求出抽奖者获奖的概率.(Ⅱ)本小题是一个超几何概型独立性实验.分布列和数学期望及方差公式.  .本题主要是考查概率知识,由生活背景引出数学知识.数学知识学以致用.
.本题主要是考查概率知识,由生活背景引出数学知识.数学知识学以致用.
试题解析:(I)设印有“美丽泉城行”标志的球有 个,不都是“美丽泉城行”标志为事件
个,不都是“美丽泉城行”标志为事件 ,
,
则都是“美丽泉城行”标志的概率是 ,由对立事件的概率:
,由对立事件的概率: ,
,
得 ,故“多彩十艺节”标志卡共有4张
,故“多彩十艺节”标志卡共有4张
∴抽奖者获奖的概率为 6分
6分
(Ⅱ) ~
~ ,
, 的分布列为
的分布列为 或
或
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
∴
 12分
12分
考点:1.概率的含义.2.对立事件.3.数学期望,数学方差的计算公式.4.独立性检验知识点.

练习册系列答案
相关题目






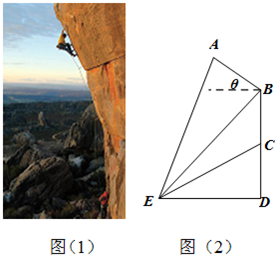 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求: