题目内容
已知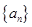 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项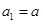 ,
,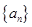 的部分项
的部分项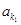 、
、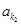 、…、
、…、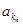 恰为等比数列,且
恰为等比数列,且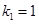 ,
,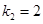 ,
,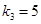 .
.
(1)求数列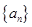 的通项公式
的通项公式 (用
(用 表示);
表示);
(2)若数列 的前
的前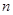 项和为
项和为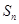 ,求
,求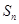 .
.
(1)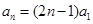 ;(2)
;(2)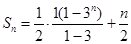
解析试题分析:(1)设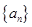 的公差为
的公差为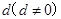 ,由
,由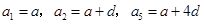 成等比数列可得方程,解出后注意检验,用等差数列通项公式可求;
成等比数列可得方程,解出后注意检验,用等差数列通项公式可求;
(2)由等差数列通项公式可表示出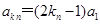 ,再由等比数列通项公式表示出
,再由等比数列通项公式表示出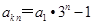 ,由其相等可得
,由其相等可得 ,然后利用分组求和可得结论;
,然后利用分组求和可得结论;
(1)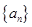 为公差不为
为公差不为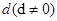 ,由已知得
,由已知得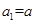 ,
,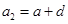 ,
,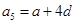 成等比数列,
成等比数列,
∴ 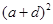
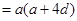 , 得
, 得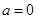 或
或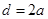
若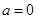 ,则
,则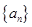 为
为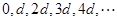 ,这与
,这与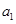 ,
,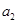 ,
,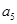 成等比数列矛盾,所以
成等比数列矛盾,所以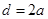 ,
,
所以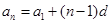
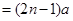 .
.
(2)由(1)可知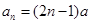 ,∴
,∴ 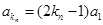 ,而等比数列
,而等比数列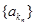 的公比
的公比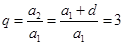 。
。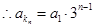 因此
因此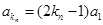
 ,
,
∴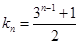 ,
,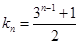
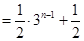
∴ 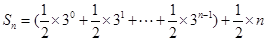
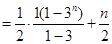
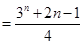
考点:等差数列,等比数列,数列求和

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
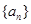 的前
的前 项和为
项和为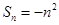 ,数列
,数列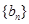 满足:
满足: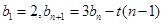 ,已知
,已知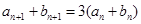 对任意
对任意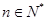 都成立
都成立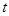 的值
的值 的前
的前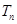 ,问是否存在互不相等的正整数
,问是否存在互不相等的正整数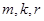 ,使得
,使得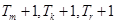 成等比数列?若存在,求出
成等比数列?若存在,求出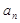 }的前
}的前 项和为
项和为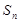 ,且满足
,且满足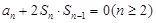 ,
,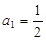 .
.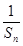 }是等差数列;
}是等差数列;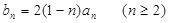 ,求证:
,求证: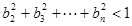 .
. 的前
的前 项和
项和 满足
满足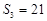 ,
,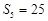 .
. 中,
中,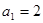 ,
,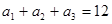 。
。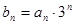 ,求数列
,求数列 的前
的前 项和
项和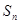
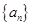 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足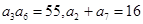 .
.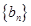 满足等式:
满足等式: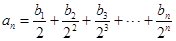 (n为正整数)求数列
(n为正整数)求数列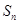 .
. 的三个内角
的三个内角 成等差数列,求证:
成等差数列,求证:
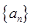 中,
中,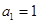 ,前
,前 项和
项和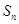 满足条件
满足条件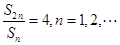 ,
, 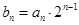 ,求数列
,求数列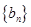 的前
的前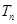 .
. 中,
中,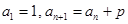 (
( 为常数,
为常数,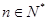 )且
)且 成公比不等于1的等比数列.
成公比不等于1的等比数列. ,求数列
,求数列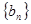 的前
的前 项和
项和 .
.