题目内容
已知集合A={x|-4≤x≤a+3}，B={x|x＜-2或x≥4}，若A∩B=A，求a的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：若A∩B=A，则A⊆B，分当a+3＜-4，即a＜-7时和当a+3≥-4，即a≥-7时两种情况讨论a的取值范围，最后综合讨论结果，可得答案
解答：
解：若A∩B=A，
则A⊆B；
当a+3＜-4，即a＜-7时，A=∅，满足条件；
当a+3≥-4，即a≥-7时，若A⊆B，
则a+3＜-2，解得a＜-5，
∴-7≤a＜-5．
综上所述，a＜-5．
故a的取值范围为（-∞，-5）．
则A⊆B；
当a+3＜-4，即a＜-7时，A=∅，满足条件；
当a+3≥-4，即a≥-7时，若A⊆B，
则a+3＜-2，解得a＜-5，
∴-7≤a＜-5．
综上所述，a＜-5．
故a的取值范围为（-∞，-5）．
点评：本题考查的知识点是集合的包含关系及应用，其中将已知转化为A⊆B，是解答的关键．
练习册系列答案
相关题目
以下四个命题中，真命题的个数是（ ）
①“若x+y=0，则x，y互为相反数”的逆命题；
②“若a＞b，则a2＞b2”的逆否命题；
③“若x=-3，则x2+x-6=0”的否命题；
④“若a+b是无理数，则a，b定为无理数”的逆命题．
①“若x+y=0，则x，y互为相反数”的逆命题；
②“若a＞b，则a2＞b2”的逆否命题；
③“若x=-3，则x2+x-6=0”的否命题；
④“若a+b是无理数，则a，b定为无理数”的逆命题．
| A、0 | B、1 | C、2 | D、3 |
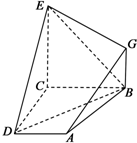如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=某几何体的三视图如图所示，则该几何体的体积为（ ）
A、4
| ||||
B、
| ||||
C、
| ||||
| D、3 |